Предмет: Геометрия,
автор: Аноним
Помогите! Докажите, что если векторы АВ и СD равны, то середины отрезков AD и ВС совпадают. Докажите обратное утверждение: если середины отрезков AD и ВС совпадают, то вектор АВ= вектору СD.
Обязательно сделайте чертеж!
Ответы
Автор ответа:
0
AB = CD => AB || CD, |AB|=|CD|
соеденим точки A и C, B и D
Получился параллелограмм так как у четырехугольника две противоположные стороны равны и параллельны. По св-ву параллелограмма, диагонали паралл. точкой пересеч-я делятся пополам. Тогда так как AD, BC - диагонали, то середины этих отрезков совпадают в точке их пересечения.
Обратное утв-ие:
Если середины отрезков AD и ВС совпадают, то вектор АВ= вектору СD
Док-во:
Достроим до 4-угольника ABCD, AD, BC-диагонали. Тогда У четырехугольника диагонали точкой пересечения делятся пополам. Следовательно это параллелограмм.
Тогда AB = CD так как их длины равны, как противоположные стороны параллелограмма, и направлены они параллельно в одну сторону.
соеденим точки A и C, B и D
Получился параллелограмм так как у четырехугольника две противоположные стороны равны и параллельны. По св-ву параллелограмма, диагонали паралл. точкой пересеч-я делятся пополам. Тогда так как AD, BC - диагонали, то середины этих отрезков совпадают в точке их пересечения.
Обратное утв-ие:
Если середины отрезков AD и ВС совпадают, то вектор АВ= вектору СD
Док-во:
Достроим до 4-угольника ABCD, AD, BC-диагонали. Тогда У четырехугольника диагонали точкой пересечения делятся пополам. Следовательно это параллелограмм.
Тогда AB = CD так как их длины равны, как противоположные стороны параллелограмма, и направлены они параллельно в одну сторону.
Приложения:
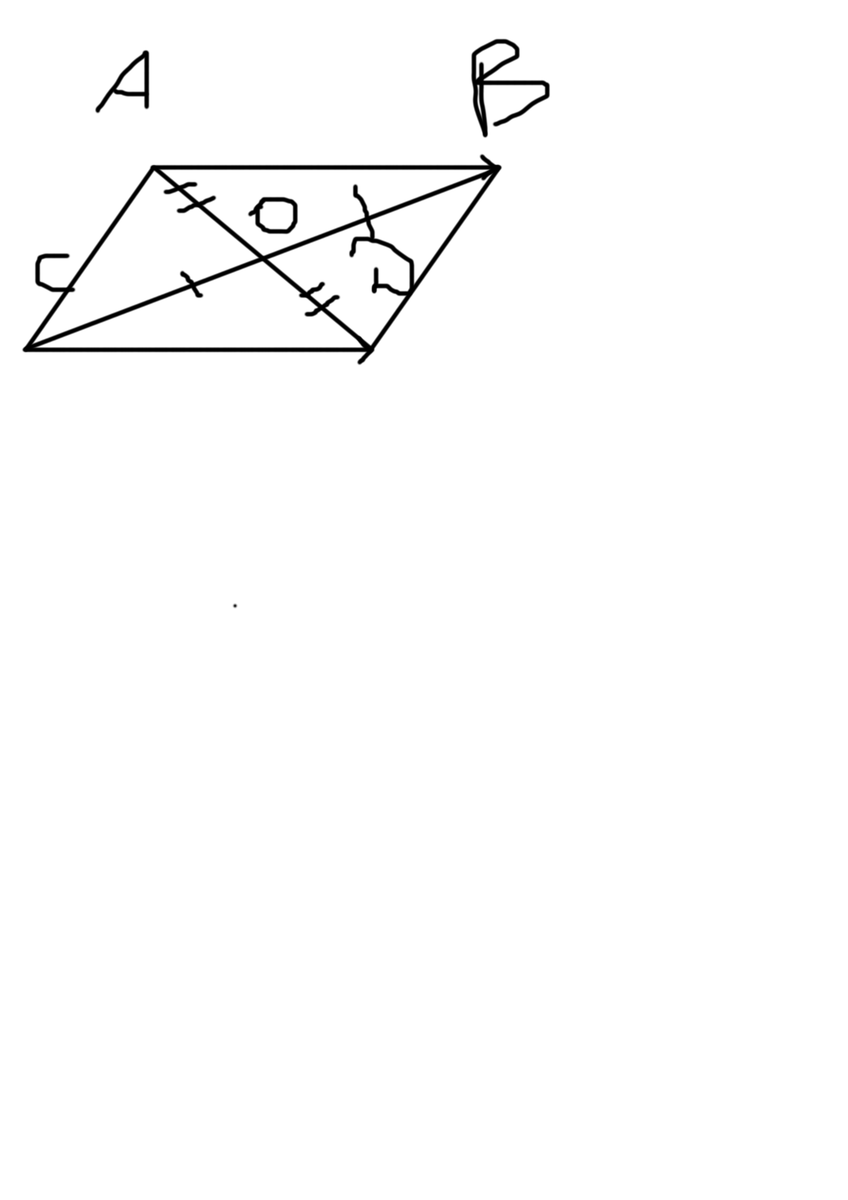
Автор ответа:
0
щас надо снять с плиты, через 5 мин дорешаю
Автор ответа:
0
можно чертеж?
Автор ответа:
0
Спасибо :)
Похожие вопросы
Предмет: Геометрия,
автор: akchurina19
Предмет: Геометрия,
автор: nikitushkinada
Предмет: Обществознание,
автор: mikelshead
Предмет: Биология,
автор: gtyty
Предмет: Физика,
автор: Five555