Question

Найти уравнение прямой, проходящей через две данные точки М1 (1,2) и М2 (3,-1).

Answer 1

M1(1;2)      M2(3;-1)
 x-x1      y-y1
------- = ---------
x2-x1     y2-y1
подставляем
x-1      y-2
----- = ------
3-1     -1-2
считаем
x-1    y-2
---- = ----
 2       -3
умножаем по диагонали
2(y-2)=-3(x-1)
2y-4=-3x+3
2y=-3x+7
     -3x+7
y= --------
         2

Answer 2

ДАНО
A(1,2) и B(3,-1) - легче будет писать формулы.
РЕШЕНИЕ
Каноническое уравнение прямой имеет вид
Y = k*x + b.
Наклон прямой - k - по формуле (от В до А)
k = ΔY/ΔX = (Ву - Ау)/(Вх - Ах) = (-1-2) : (3-1) = -3/2
Сдвиг по оси У - b по формуле
Ву = k*Bx + b - отсюда
b = By - k*Bx = -1 - (-3/2)*3 = -1+9/2 = 3 1/2
Окончательно уравнение прямой
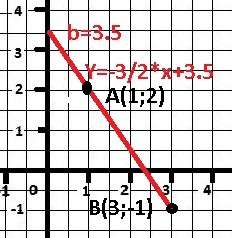
Y = - 3/2*x + 3 1/2 - каноническая форма уравнения прямой - ОТВЕТ
3*х + 2*у = 7 - параметрическая форма записи. - ОТВЕТ
Рисунок к задаче в приложении.

Answer 3

У меня такие варианты ответов к этому заданию: 1.3x + 2y + 1 = 0
2.3x – 2y + 1 = 0
3. 3x + 2y + 9 = 0
4. 3x +2 y 7 = 0

Answer 4

Какие ещё варианты. Через две точки проходит ОДНА прямая.

Answer 5

эти варианты из задания. в котором нужно выбрать один правильный ответ из предложенных

Answer 6

ОТВЕТ 4 - 3х+2у-7 = 0

Answer 7

спасибо