Предмет: Геометрия,
автор: dzp10625
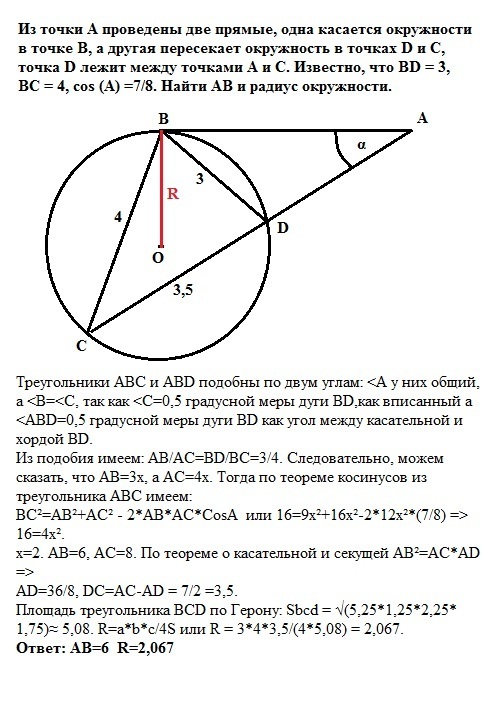
Из точки А проведены две прямые, одна касается окружности в точке В, а другая пересекает окружность в точках D и C, точка D лежит между точками А и С. Известно, что BD = 3, BC = 4, cos (А) =7/8. Найти АВ и радиус окружности
Ответы
Автор ответа:
0
Треугольники АВС и АВD подобны по двум углам: <A у них общий, а <B=<C, так как <C=0,5 градусной меры дуги BD,как вписанный а <ABD=0,5 градусной меры дуги BD как угол между касательной и хордой BD. Из подобия имеем: АВ/АС=BD/BC=3/4. Следовательно, можем сказать, что АВ=3х, а АС=4х. Тогда по теореме косинусов из треугольника АВС имеем: ВС²=АВ²+АС² - 2*АВ*АС*CosA или 16=9х²+16х²-2*12х²*(7/8) => 16=4х². х=2. АВ=6, АС=8. По теореме о касательной и секущей АВ²=АС*AD => AD=36/8, DC=AC-AD = 7/2 =3,5. Площадь треугольника BCD по Герону при полупериметре р=5,25:
Sbcd = √(5,25*1,25*2,25*1,75)≈ 5,08.
R=a*b*c/4S или R = 3*4*3,5/(4*5,08) = 2,067.
Ответ: АВ=6, R=2,067.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: marinarybakova8989
Предмет: Алгебра,
автор: iskatel13
Предмет: Литература,
автор: nastyabol1988krl
Предмет: Математика,
автор: риса11
Предмет: Математика,
автор: PulsePro