Предмет: Алгебра,
автор: TequilaSunrise
помогите, пожалуйста :)
Приложения:
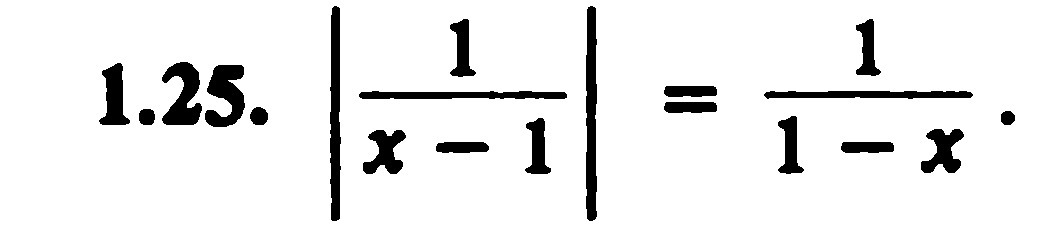
Ответы
Автор ответа:
0
ОДЗ:
Нуль подмодульного выражения:
Значит решения рассматриваем на интервалах:
С учетом ОДЗ
C учетом ОДЗ
нет решений
Ответ:
Похожие вопросы
Предмет: Математика,
автор: lena28741
Предмет: Математика,
автор: ira000167
Предмет: Английский язык,
автор: LordLuntik
Предмет: Биология,
автор: ятсан1
Предмет: Химия,
автор: alisikanastasik