Предмет: Геометрия,
автор: ilyamirzaev
В окружность вписан квадрат со стороной 8 см найдите сторону правильного окружности шестеугольника описанного около этой окружности
Ответы
Автор ответа:
0
Вершины вписанного квадрата лежат на описанной около него окружности. Диагональ квадрата - диаметр этой окружности.
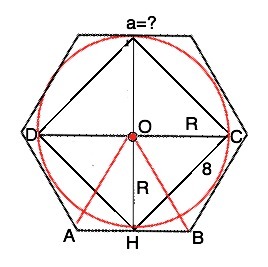
Диагональ вписанного квадрата со стороной 8 см по теореме Пифагора DC=√(DH²+CH²) или DC=СН:sin45°=8√2, ⇒ радиус ОН =D:2=4√2 см. (См. рисунок). Соединим вершины А и В шестиугольника с центром О вписанной в него окружности.
Центральный угол АОВ=360°:6=60°, треугольник АОВ - равносторонний. Радиус вписанной окружности является его высотой. сторона АВ=АО=ОН:sin60°=(4√2):√3/2=(8√2):√3 или см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sofia1710208
Предмет: Музыка,
автор: ksatrova5
Предмет: Математика,
автор: vall31770
Предмет: Математика,
автор: 230605010909
Предмет: Обществознание,
автор: inochkafilatov