Предмет: Алгебра,
автор: Аноним
Найти область определения функции y=квадратный корень из 2 cos 3x -1?
Ответы
Автор ответа:
0
y = sqrt(2*cos(3x) - 1) - такая запись?
ОДЗ: подкоренное выражение всегда неотрицательное, косинус всегда лежит на отрезке [-1;1]
2*cos(3x) - 1>=0, cos(3x)>=1/2
-1<=cos(3x)<=1
Общее решение (пересечение): 1/2 <=cos(3x)<=1
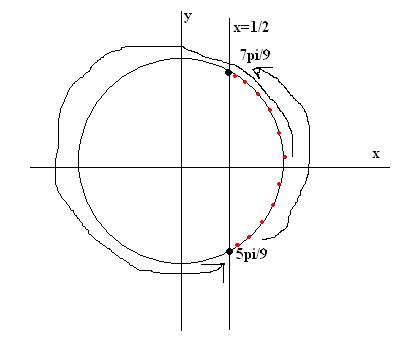
cos(3x) >= 1/2
5pi/3 + 2pi*k <= 3x <= 7pi/3 + 2pi*k
5pi/9 + 2pi*k/3 <= x <= 7pi/9 + 2pi*k/3
P.S. На картинке попыталась показать, как получены эти значения
ОДЗ: подкоренное выражение всегда неотрицательное, косинус всегда лежит на отрезке [-1;1]
2*cos(3x) - 1>=0, cos(3x)>=1/2
-1<=cos(3x)<=1
Общее решение (пересечение): 1/2 <=cos(3x)<=1
cos(3x) >= 1/2
5pi/3 + 2pi*k <= 3x <= 7pi/3 + 2pi*k
5pi/9 + 2pi*k/3 <= x <= 7pi/9 + 2pi*k/3
P.S. На картинке попыталась показать, как получены эти значения
Приложения:
Похожие вопросы
Предмет: Математика,
автор: semencukkata69
Предмет: История,
автор: didukulana
Предмет: Математика,
автор: potaturkinoleg93
Предмет: Алгебра,
автор: KittiMelnikovaa