Question

Кулю радіуса r вписали в конус висотою H і радіуса основи R. Установить відповідність між висотою H і радіусом основи R конуса (1-4) та радіусом r кулі (А-Д).
1) 4 см, 3 см; А) 6 см;
2) 16 см, 12 см; Б) 3 см;
3) 24 см, 7 см; В) 1,5 см;
4) 8 см, 6 см; Г) 21/4 см;
Д) 3 см.

Answer 1

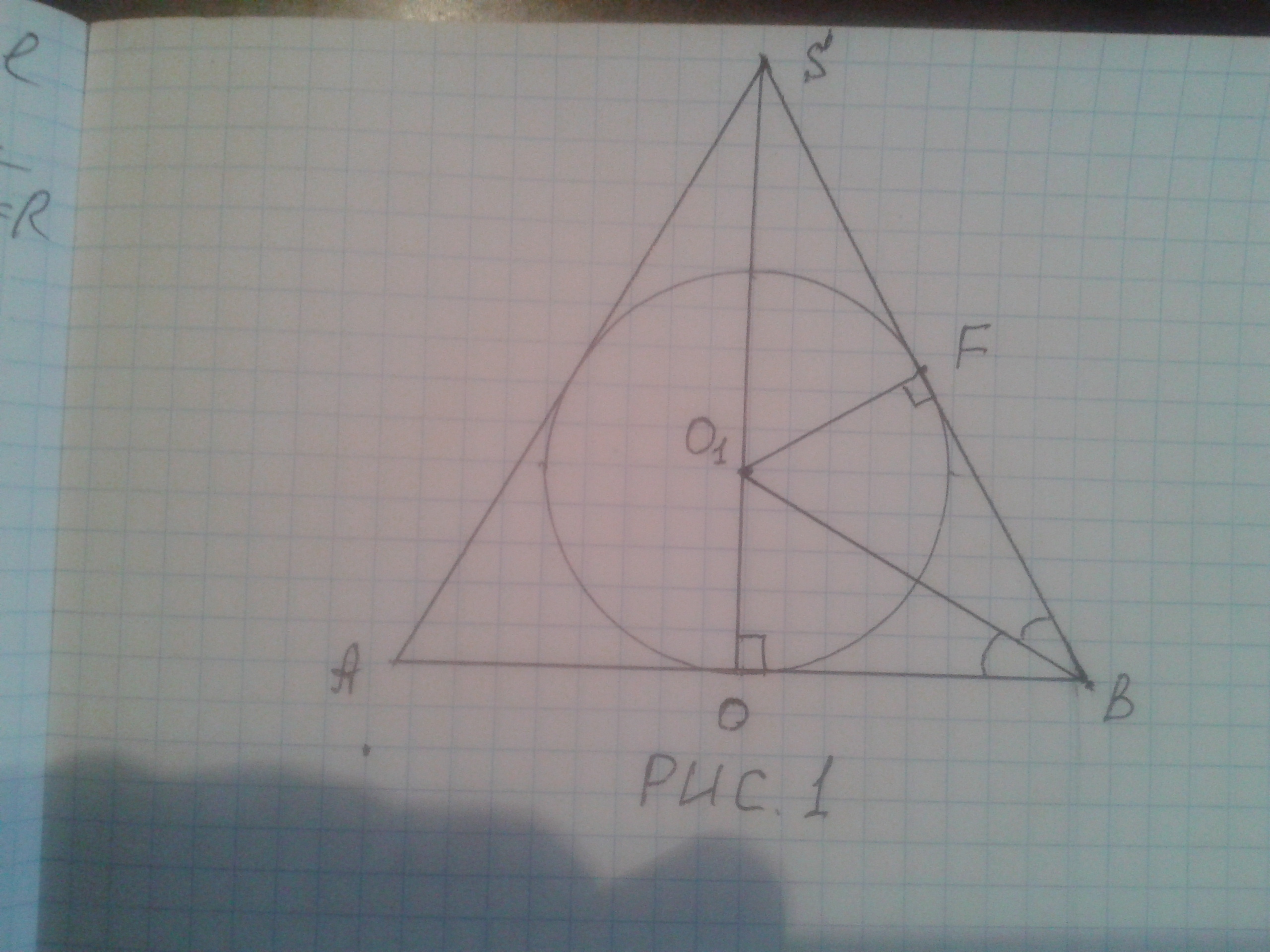
Рассмотрим сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара (Рис. 1). 
Для данного треугольника образующие SA=SB=L. Высота конуса SO=H. Радиус вписанного шара ОО₁=O₁F=r, a радиус основания конуса ОВ=R. Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:
SB/SO₁=OB/OO₁   ⇒
L/(H-r)=R/r.
По теореме Пифагора:
SB=√(SO²+OB²)   ⇒    L=√(H²+R²).
Таким образом:
√(H²+R²)/(H-r)=R/r
Подставляя различные комбинации соотношений получаем ответ.
Ответ: 1)В), 4)Б), 4)Д).

Answer 2

Велике Вам спасибі, Ви мені дуже допомогли!)))

Answer 3

Удачи.