Предмет: Алгебра,
автор: Аноним
Степень с рациональным показателем
Приложения:

Ответы
Автор ответа:
0
учись, ничего сложного, ФСУ и свойства степеней
Приложения:
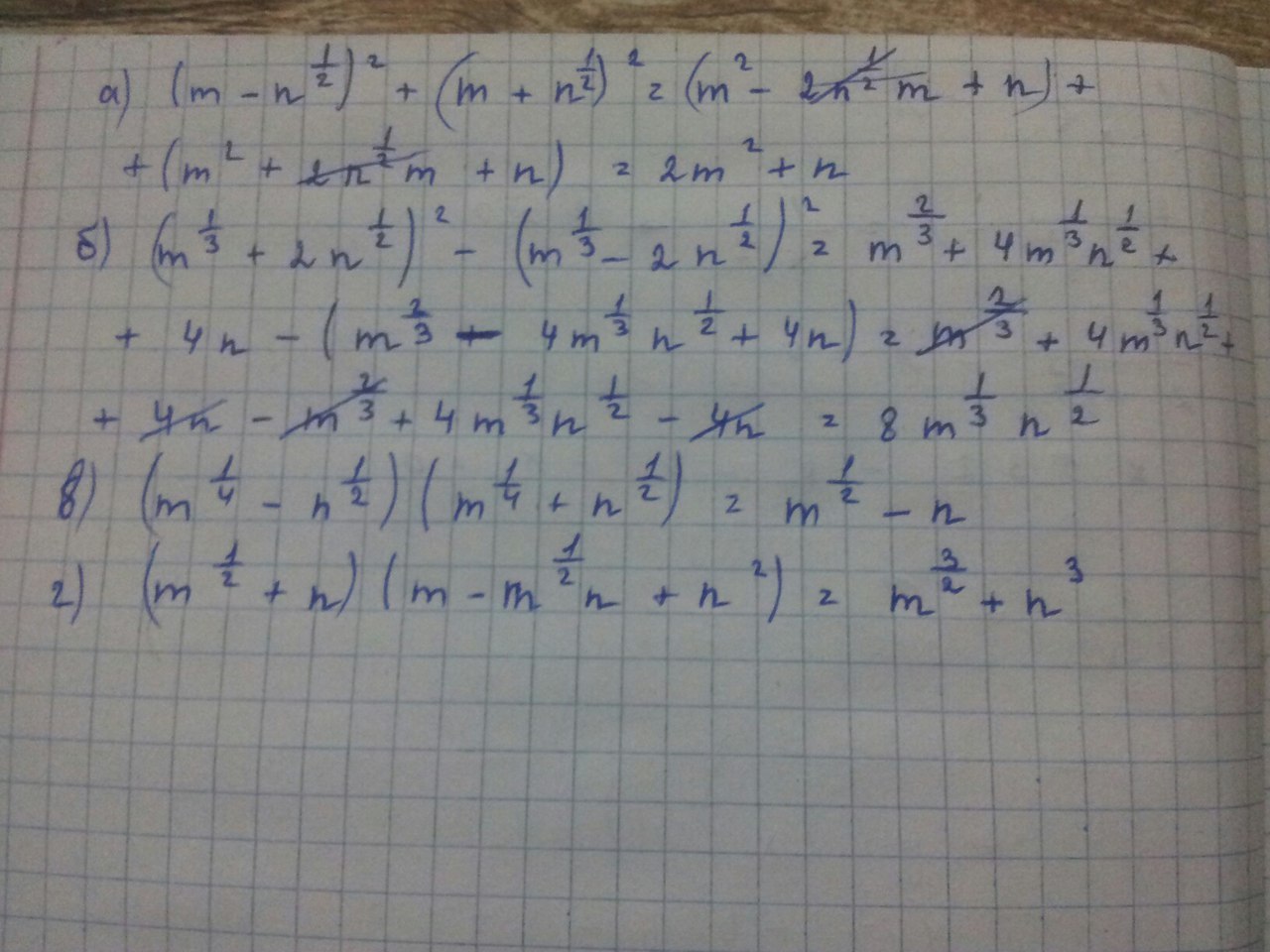
Автор ответа:
0
в первом задании в ответе 2n
Автор ответа:
0
да спасибо я уже заметила)
Автор ответа:
0
a) 

б)

в)
г)
б)
в)
г)
Приложения:
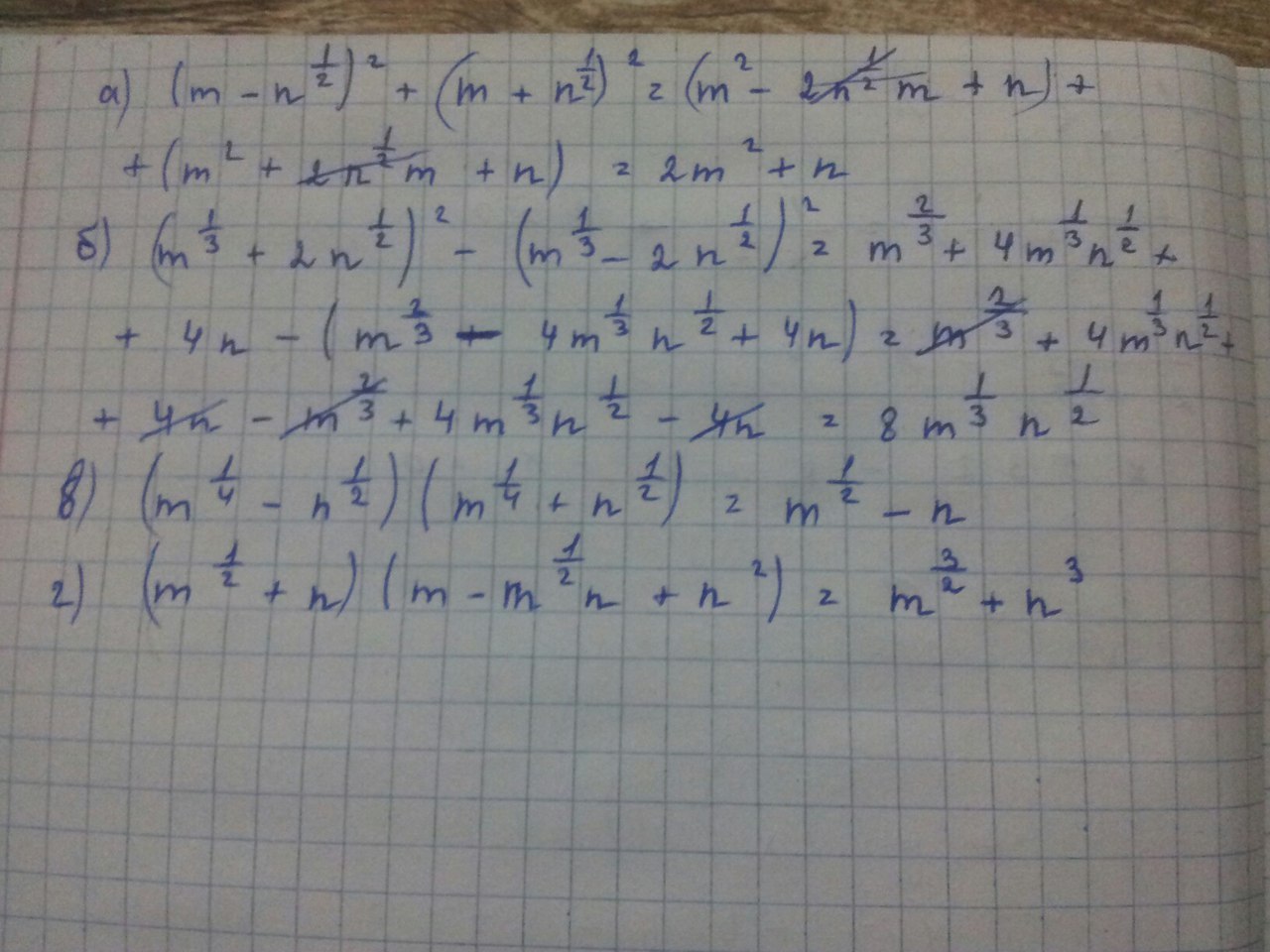
Похожие вопросы
Предмет: Литература,
автор: dashaspace
Предмет: Геометрия,
автор: belaruskh12
Предмет: Литература,
автор: llinnna15
Предмет: Математика,
автор: smoleva2001
Предмет: Биология,
автор: Аноним