Question

1)
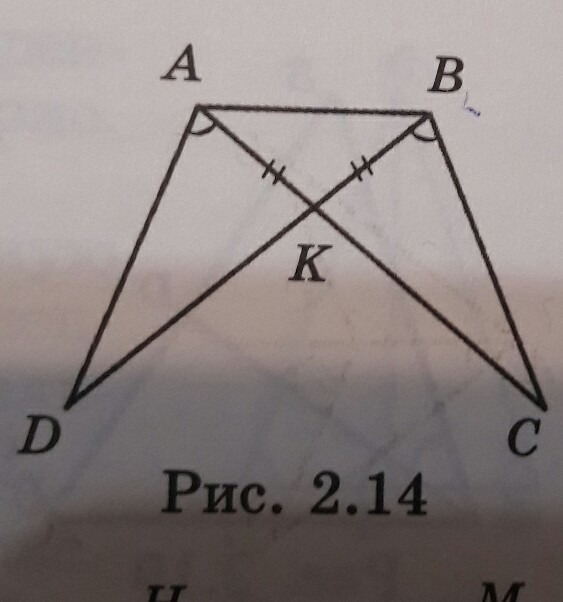
На рисунке 2.14 угол DAC = DBC, AK = KB. Докажите, что угол DAB = CBA
2)
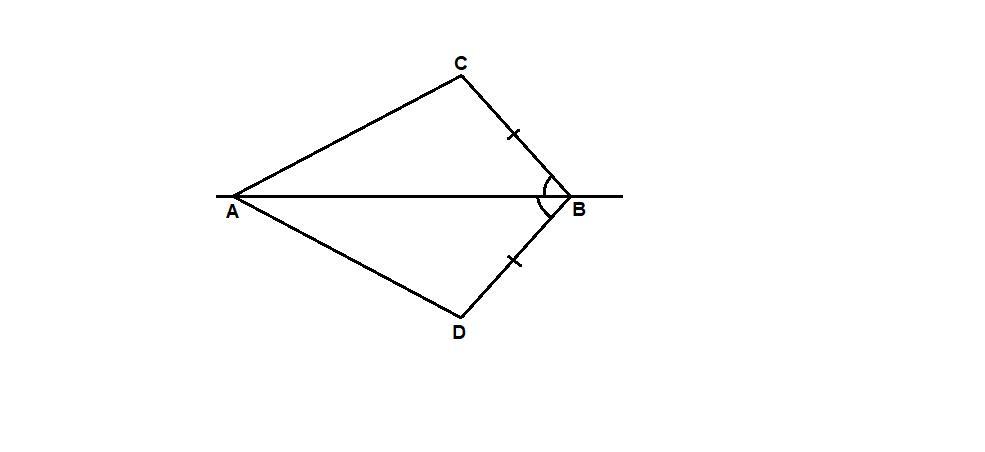
Точки C и D расположены по разные стороны от прямой AB так,что угол ABC=углу ABD. BD=BC. Докажите что AB- биссектриса угла DAC.

Answer 1

Ответ:

1) АК = КВ, значит ΔАКВ равнобедренный,

∠КАВ = ∠КВА как углы при основании равнобедренного треугольника.

∠DAB = ∠DAC + ∠KAB

∠CBA = ∠DBC + ∠KBA

Углы DAC и DBC равны по условию, ∠КАВ = ∠КВА (см. выше), значит и

∠DAB = ∠СВА

2) BD = BC по условию,

∠ABC = ∠ABD по условию,

АВ - общая сторона для треугольников ABC и ABD, значит

ΔABC = ΔABD по двум сторонам и углу между ними.

В равных треугольниках напротив равных сторон лежат равные углы, значит ∠CAB = ∠DAB, а это значит, что

АВ - биссектриса угла DAC.