Предмет: Геометрия,
автор: Matilda1337
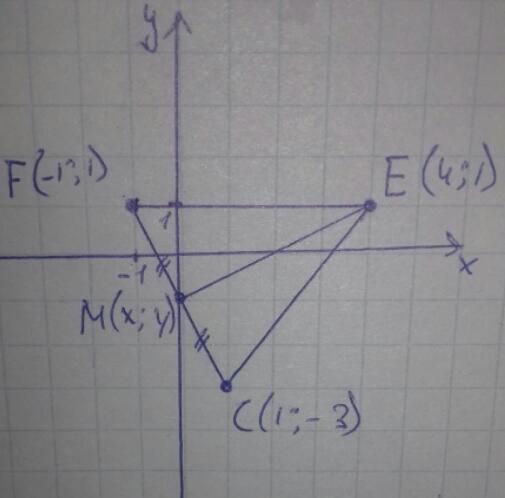
Треугольник fec задан координатами своих вершин f(-1;1), e(4;1), c(1;3)
a) докажите что ФЕК-равнобедренный.
Б) найдите медиану проведенную из вершины Е.
Ответы
Автор ответа:
0
Смотри условие и рисунок к задачи внизу.
Найдём стороны треугольника.
FE=EC≠CF ⇒ ΔFEC равнобедренный.
Медиана из верщины Е это отрезок соединяющий середину FC и точку Е.
Найдём координаты М, середины FC. Затем саму медиану EM.
Ответ: ЕМ = 2√5.
Приложения:

Похожие вопросы