Предмет: Алгебра,
автор: m1neevaa
помогите пожалуйста,можно с развёрнутым ответом.
Приложения:
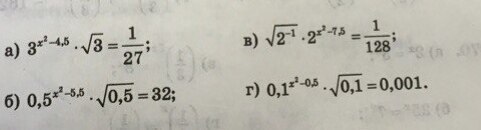
Ответы
Автор ответа:
0
Задание на показательные уравнение. Для понимая, что вообще происходит нужно знать основные определения и свойства.
приведу несколько из них

Причем важно помнить,что
Решим 1 номер



Соберем слева в 1 тройку

Теперь вспоминаем такое пр-ло, что если основания (показатели) одинаковые, то их можно отбросить и смотреть только на степени.
Т.е.
Итого получаем следующее уравнение

В пункте б аналогично, приводим , а
, а 
Впрочем они все аналогичны, просто не забывайте о правилах решения таких задач.
приведу несколько из них
Причем важно помнить,что
Решим 1 номер
Соберем слева в 1 тройку
Теперь вспоминаем такое пр-ло, что если основания (показатели) одинаковые, то их можно отбросить и смотреть только на степени.
Т.е.
Итого получаем следующее уравнение
В пункте б аналогично, приводим
Впрочем они все аналогичны, просто не забывайте о правилах решения таких задач.
Похожие вопросы
Предмет: Литература,
автор: nika961181
Предмет: История,
автор: samkagoha
Предмет: История,
автор: elnursapiolla
Предмет: Математика,
автор: Pont4ik
Предмет: Алгебра,
автор: 1212Юлька1212