Предмет: Математика,
автор: AnnBernstein
Даны вершины треугольника ABC. Найти:
1. уравнение стороны ab
2. уравнение высоты Ch
3. уравнение медианы am
4. точку n пересечения медианы am и высоты Ch
5. уравнение прямой, проходящей через вершину C параллельно стороне ab
6. расстояние от точки c до прямой ab
Координаты вершин : A(-4;2) B(8;-6); C(2;6)
Ответы
Автор ответа:
0
1) Уравнение стороны
Откуда после вычитания второго из первого получим
2) Прямые, заданные уравнениями
Нам же нужно найти уравнение прямой, которая перпендикулярна прямой
3) Медиана
Получается, что медиана проходит через точки
Откуда получаем
Значит, медиана задаётся уравнением
4) Точку пересечения
Получили, что медиана
5) Семейство прямых, параллельных прямой
Решаем соответствующее уравнение:
Получили, что нужная нам прямая задаётся уравнением
6) Расстояние от точки
Подставляем:
Приложения:
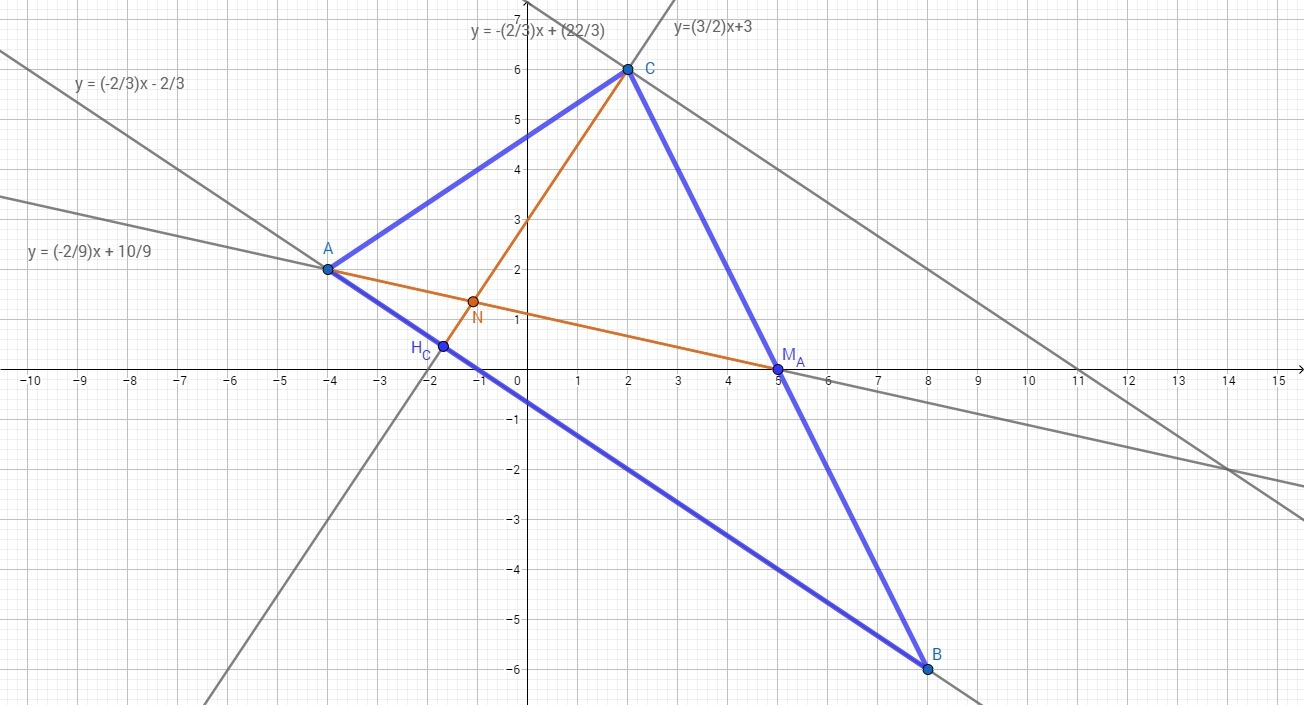
Похожие вопросы
Предмет: Алгебра,
автор: Lem1one
Предмет: Биология,
автор: Аноним
Предмет: Физика,
автор: darkbdhdhd
Предмет: География,
автор: slavablago
Предмет: Информатика,
автор: vikusiklady05