Question

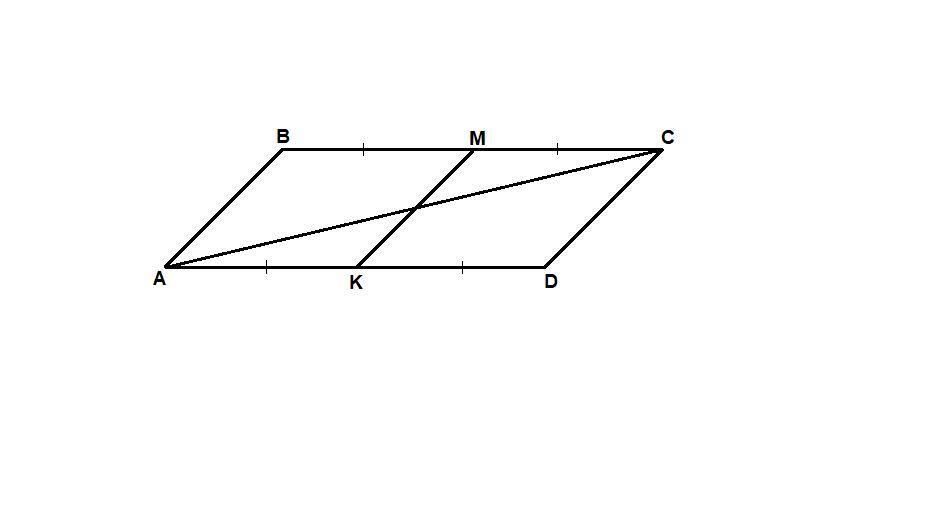
В параллелограмме ABCD точки M и K-середины сторон BC и AD соответственно. Докажите, что площадь четырёхугольника ABMK равна площади треугольника ABC. СРОЧНО!!!! С РИСУНКОМ!!!

Answer 1

Объяснение:

АК = 1/2 AD

BM = 1/2 BС,

а так как в параллелограмме противоположные стороны равны, то

АК = ВМ.

АК ║ ВМ, так как лежат на параллельных сторонах, значит

АВМК - параллелограмм.

Площадь параллелограмма можно найти как произведение двух сторон на синус угла между ними:

Sabmk = AB · BM · sin∠B = АВ · 1/2 ВС · sin∠B = 1/2 AB · BC · sin∠B

Площадь треугольника можно найти как половину произведения двух сторон на синус угла между ними:

Sabc = 1/2 AB · BC · sin∠B ⇒

Sabmk = Sabc