Предмет: Алгебра,
автор: Armagggedon11
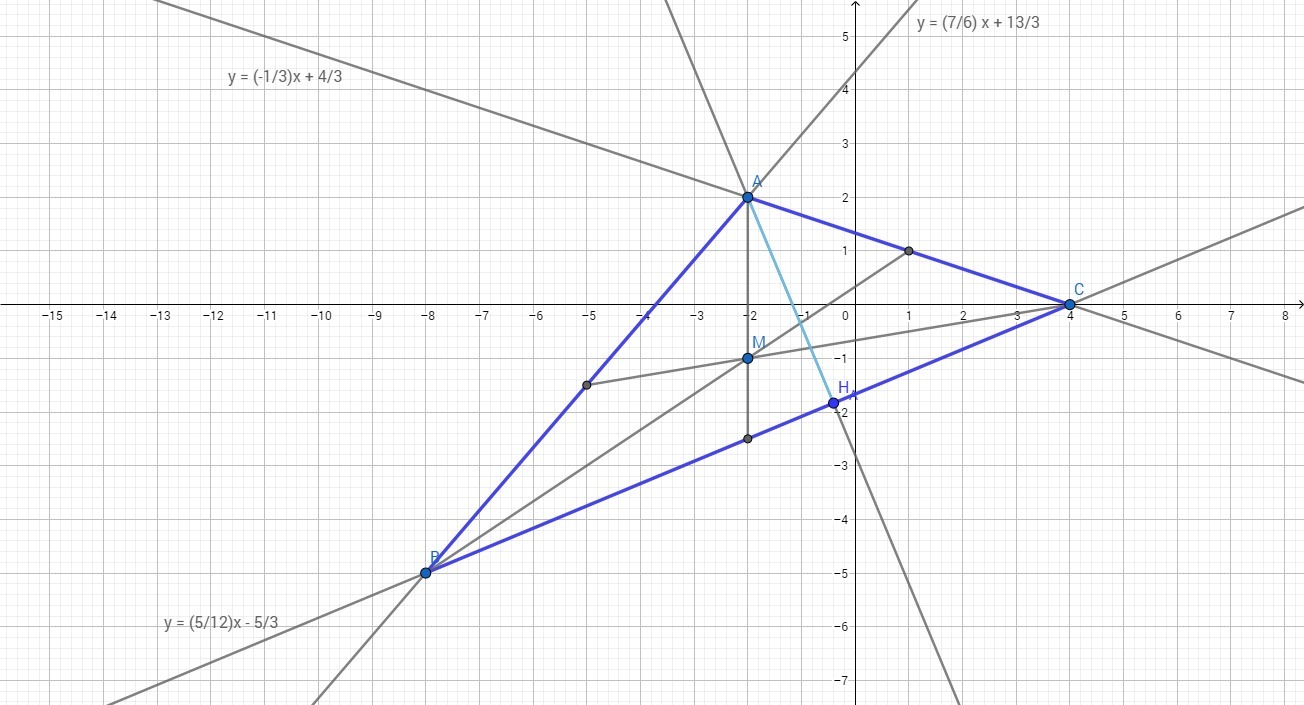
Построить треугольник
Приложения:

Ответы
Автор ответа:
0
1)
Прямая
Найдём уравнение этой прямой, решив систему уравнений:
Откуда
Прямая
Найдём уравнение этой прямой, решив систему уравнений:
Откуда
Прямая
Найдём уравнение этой прямой, решив систему уравнений:
Откуда
2)
Координаты точки
Значит, точка пересечения медиан имеет следующие координаты:
3)
Расстояние от точки
Уравнение стороны
Расстояние от точки
4) Площадь треугольника равна полупроизведению высоты на основание, на которое опущена высота. Конкретно в нашем треугольнике:
Длину
Приложения:
Автор ответа:
0
Огромное спасибо
Похожие вопросы
Предмет: Математика,
автор: angelalex200911
Предмет: Математика,
автор: nastya666sukrusheva
Предмет: История,
автор: nadagusina1709
Предмет: Математика,
автор: руся82
Предмет: Биология,
автор: Skil86Russian