Question

Угол при основании равнрбедренного треугольника=30(градусов),боковая сторона=10см.Найдите диаметр окружности описанной около треугольника.

Answer 1

Такс, с чего начать. Вообще радиус окружности считается по формуле r=p-c, где p -полупериметр треугольника в нашем случае, с - гипотенуза треугольника. 
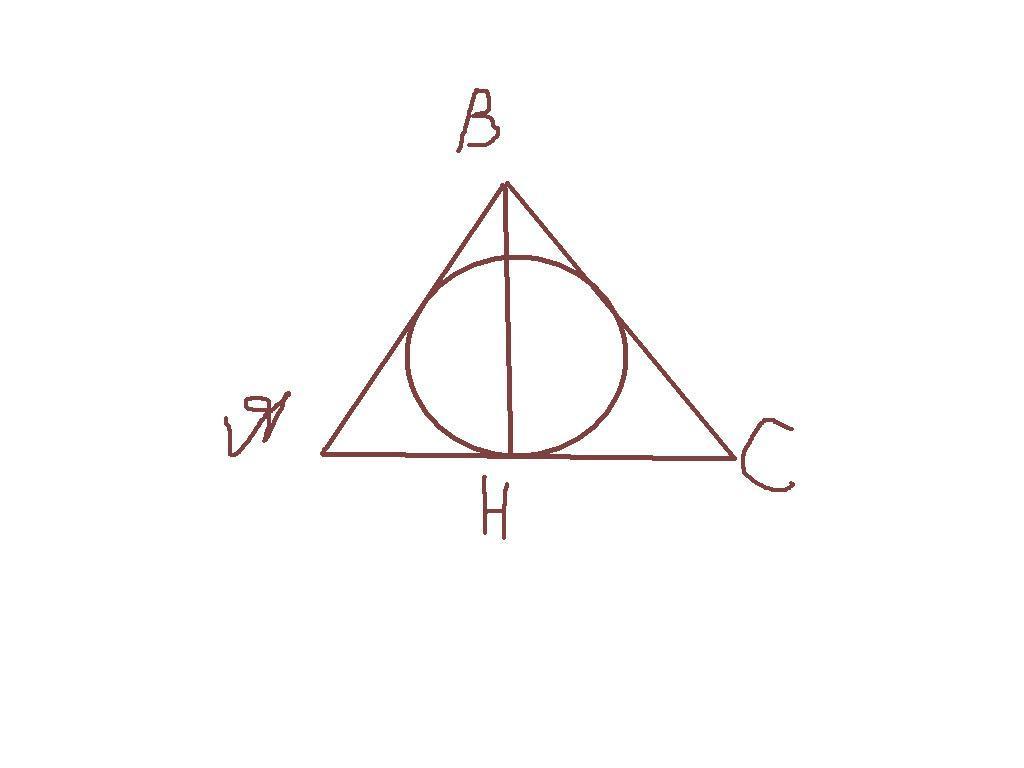
Проведем высоту BH. 
Треугольник ABH - прямоугольный. Т.к. по условию задачи угол BAH = 30 градусов, то BH = 12 AB = 5 см. 
По теореме Пифагора: AH2=Ab2 - BH2
AH = корень из 75 = 5 корней из 3 см. 
Т.к. треугольник ABC равнобедренный, то BH  - высота, медиана, значит AH = HC
AC = AH+HC = 10 корней из 3 см.
p = 12 P = AB+BC+AC = (10+10+10 корней из 3) :2 = 10 корней из 3 см2.
Найдем радиус: r = 10 корней из 3 - 10 = 10 - 10 корней из 3 см.