Предмет: Математика,
автор: quinte
Приложения:
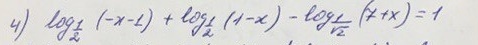
Ответы
Автор ответа:
0
Log
Log ∞
∞
∞
 ∞
∞
∞+∞-
 ∞
∞
∞+∞-∞=1
Упрощаем
∞=1
Поскольку ∞=1 не верно
Ответ: Нет решений
Log
∞
∞+∞-
∞+∞-∞=1
Упрощаем
∞=1
Поскольку ∞=1 не верно
Ответ: Нет решений
Автор ответа:
0
Точно основание у Логарифма чуть выше чем обычно, ни чего страшного, ответ от этого не изменится, и знак бесконечности почему то стоит чуть ниже знака =, а должно быть на одном уровне
Автор ответа:
0
Решение неверно.
Автор ответа:
0
если не сложно можешь уточнить место где я ошиблась?
Похожие вопросы
Предмет: Геометрия,
автор: nastia20vas08
Предмет: Алгебра,
автор: viarrvolkova
Предмет: Математика,
автор: pidorgeev
Предмет: Математика,
автор: jis22w
Предмет: Математика,
автор: den185