Предмет: Алгебра,
автор: 007gaglik
Решите пожалуйста производную сложной функции.
Приложения:
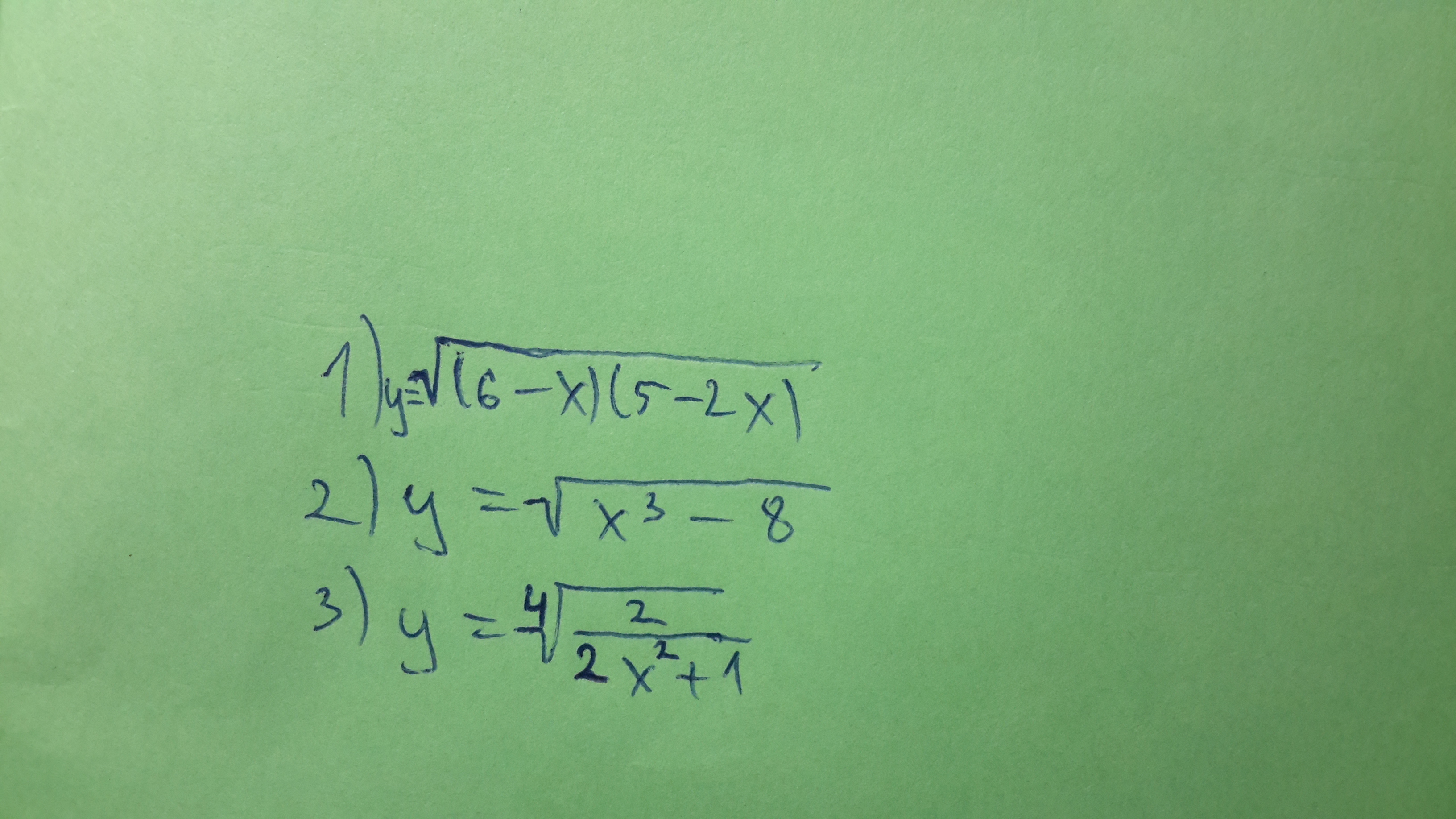
Ответы
Автор ответа:
0
2)
3)
Похожие вопросы
Предмет: Алгебра,
автор: kbratanov275
Предмет: Геометрия,
автор: reoeksandr556
Предмет: Русский язык,
автор: alenagrazeva498
Предмет: Математика,
автор: Enjoy58
Предмет: География,
автор: missisprusacko