Предмет: Математика,
автор: romanrogovenko
Помогите решить 2 примера
Приложения:
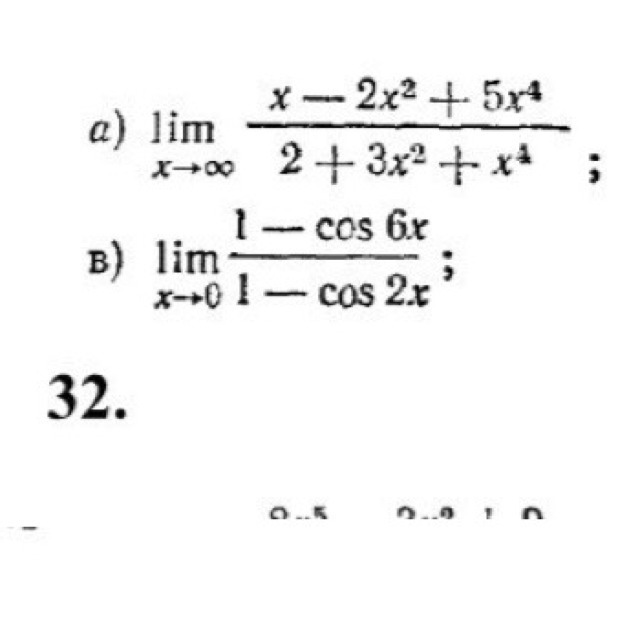
Ответы
Автор ответа:
0
В первом случае мы просто делим числитель и знаменатель на  :
:

Во втором случае мы по правилу Лопиталя дифференцируем числитель и знаменатель дважды:

Во втором случае мы по правилу Лопиталя дифференцируем числитель и знаменатель дважды:
Автор ответа:
0
второе не верно производную взял
Автор ответа:
0
сейчас исправлю
Автор ответа:
0
спасибо
Автор ответа:
0
Не могли бы вы написать это на листе , а то не очень понятно
Автор ответа:
0
Я больше не могу добавлять ответов к этому вопросу, но ты можешь нажать на картинку правой кнопкой мыши, открыть её в новой вкладке и там уже увеличить. Может поможет.
Похожие вопросы
Предмет: Алгебра,
автор: miko25420
Предмет: Русский язык,
автор: ekbdbekajshhsajjs
Предмет: Алгебра,
автор: zdraste52
Предмет: Физика,
автор: Аноним
Предмет: Химия,
автор: рлааид