Предмет: Математика,
автор: Аноним
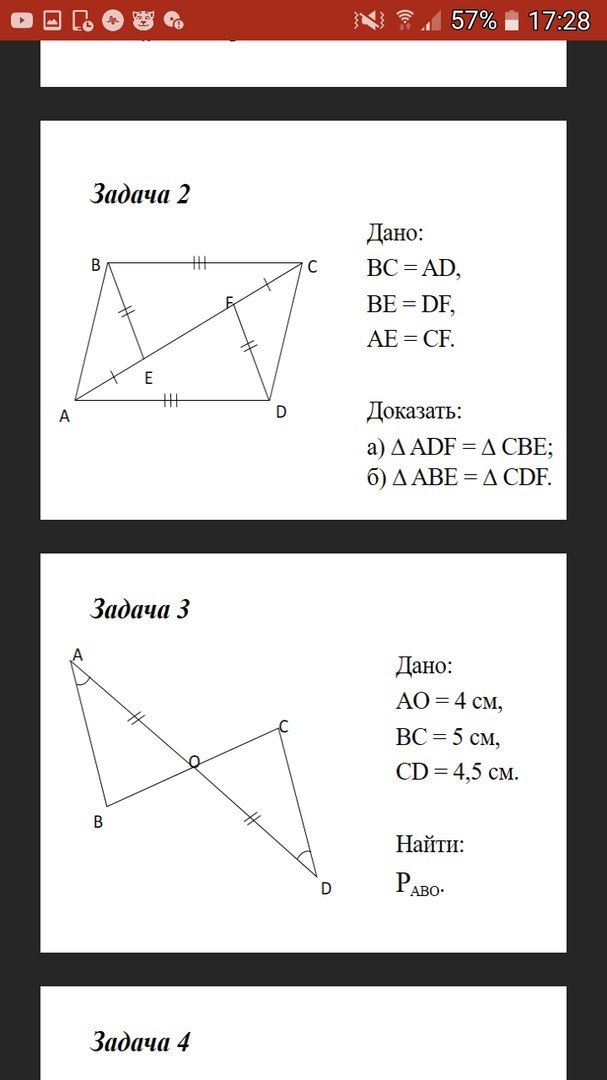
Задача 2. Решите только под Б)
Приложения:
Ответы
Автор ответа:
0
т.ADF=т.CEB по третьему признаку (так как стороны равны по условию, а часть EF общая)
исходя из этого получаем что у.CFD смежный у.AFD, также и с другой стороны у.BEA смежный у.CEB. Така треугольники найденные раннее равны то и их углы тоже, а значит смежные их углам тоже равны.
Делаем вывод, т.CFD=т.AEB по первому признаку.
("т."-треугольник, "у."-угол, первый признак-сторона,угол,сторона; третий признак-сторона,сторона,сторона)
исходя из этого получаем что у.CFD смежный у.AFD, также и с другой стороны у.BEA смежный у.CEB. Така треугольники найденные раннее равны то и их углы тоже, а значит смежные их углам тоже равны.
Делаем вывод, т.CFD=т.AEB по первому признаку.
("т."-треугольник, "у."-угол, первый признак-сторона,угол,сторона; третий признак-сторона,сторона,сторона)
Автор ответа:
0
можете не благодарить, но если поставите спасибо, буду рад))
Автор ответа:
0
Рассмотрим ABDC:
углы BCA и CAB равны из равенства треугольников ADF и CBE. из этого следует, что BC и AD параллельные прямые, а AC секущая.из этого следует что равны смежные с BCA и CAB углы. 180 - x - y = z в обеих случаях, а это значит что углы B и D равны как и углы A и C из этого следует , что фигура параллелограмм и по св-ву параллелограмма AB = CD. Треугольники ABE и CDF равны по третьему признаку равенства треугольников.
углы BCA и CAB равны из равенства треугольников ADF и CBE. из этого следует, что BC и AD параллельные прямые, а AC секущая.из этого следует что равны смежные с BCA и CAB углы. 180 - x - y = z в обеих случаях, а это значит что углы B и D равны как и углы A и C из этого следует , что фигура параллелограмм и по св-ву параллелограмма AB = CD. Треугольники ABE и CDF равны по третьему признаку равенства треугольников.
Похожие вопросы
Предмет: Психология,
автор: alexandrovnaaa69
Предмет: Информатика,
автор: sirko172002
Предмет: Музыка,
автор: sasha6949
Предмет: Математика,
автор: heysss
Предмет: Обществознание,
автор: KaratishkaJake