Question

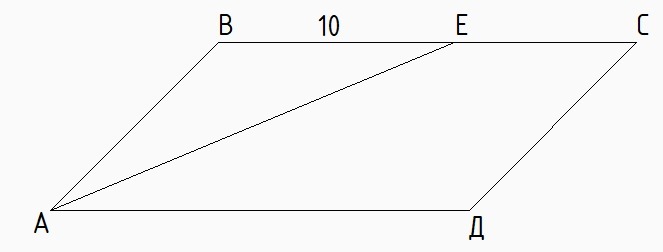
В параллелограмме ABCD проведена биссектриса угла BAD,которая пересекает сторону BC в точке E .
А -докажите что треугольник АВЕ- равнобедренный,
б-найдите сторону AD ,если ВЕ=10см,Периметр abcd =62см.

Answer 1

В параллелограмме ВС || АД
и углы ЕАД и АЕВ равны как накрест лежащие при секущей АЕ
Углы ЕАД и ЕАВ равны как углы, образованные биссектрисой угла А.
Итого - в треугольнике АВЕ угол А равен углу Е => треугольник равнобедренный
Теперь с периметром
ВЕ = 10 см
АВ = 10 см как вторая сторона равнобедренного  треугольника
СД = АБ как противоположные стороны параллелограмма
ВС = АД тоже как стороны параллелограмма
Итого
2*АД + 2*10 = 62
АД + 10 = 31
АД = 21 см