Предмет: Геометрия,
автор: Аноним
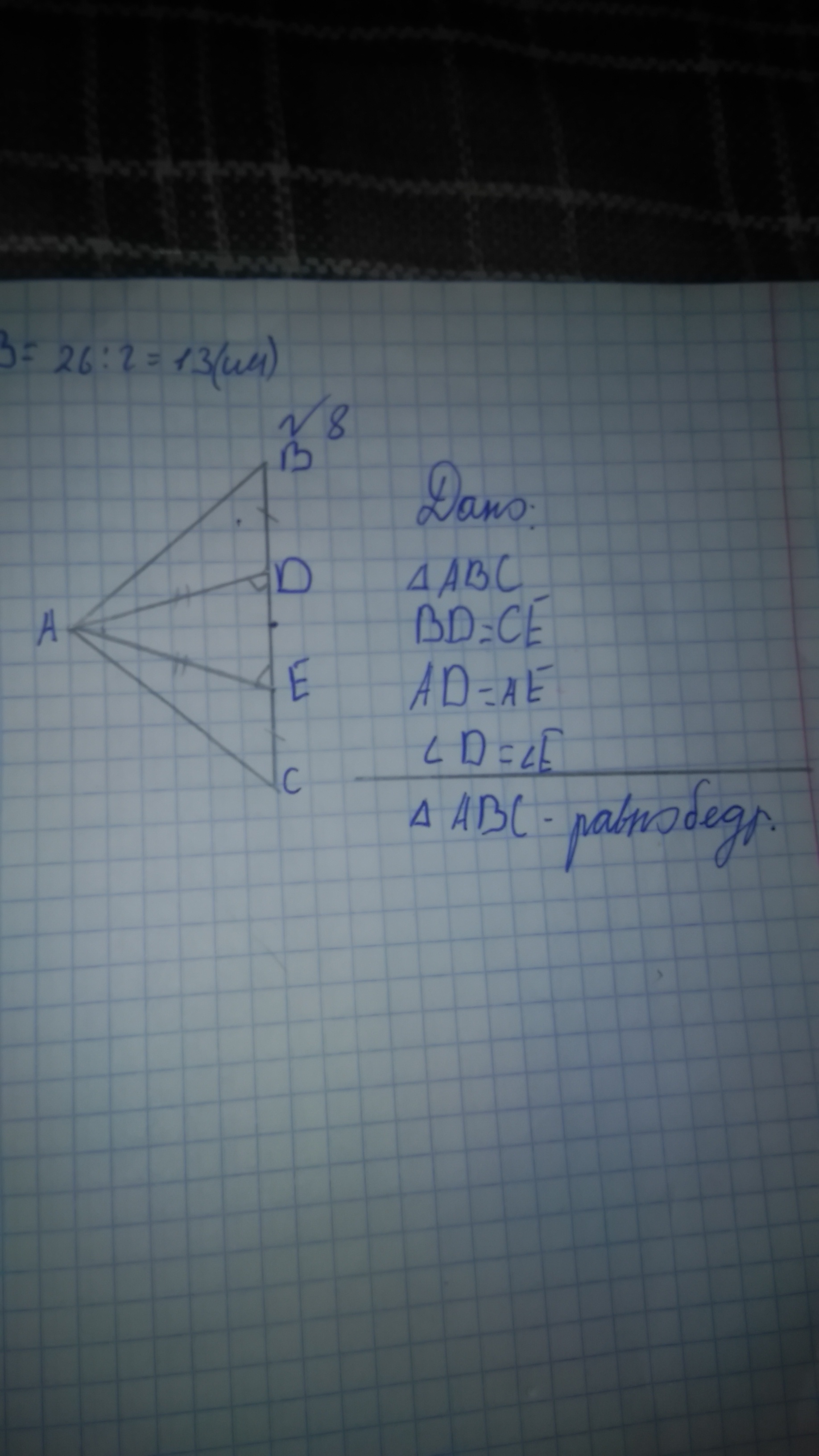
Дано: треугольник ABC, BD=CE, AD=AE,угол D равен углу E. Доказать что треугольник равнобедренный.
Приложения:
Ответы
Автор ответа:
0
Пусть ∠D = ∠E = x, тогда:
∠АЕС = 180 - х и ∠ADB = 180 - х , следовательно ∠АЕС = ∠ADB
Рассмотрим треугольники AВD и AСE:
BD=CE
AD=AE
∠АЕС = ∠ADB
следовательно ΔAВD = ΔAСE (по двум сторонам и углу между ними).
В равных треугольниках соответствующие стороны равны, значит АВ = АС, следовательно ΔАВС равнобедренный, что и требовалось доказать.
∠АЕС = 180 - х и ∠ADB = 180 - х , следовательно ∠АЕС = ∠ADB
Рассмотрим треугольники AВD и AСE:
BD=CE
AD=AE
∠АЕС = ∠ADB
следовательно ΔAВD = ΔAСE (по двум сторонам и углу между ними).
В равных треугольниках соответствующие стороны равны, значит АВ = АС, следовательно ΔАВС равнобедренный, что и требовалось доказать.
Похожие вопросы
Предмет: Информатика,
автор: tanboyar
Предмет: Обществознание,
автор: lerikannenkova
Предмет: Физика,
автор: ulas123456713
Предмет: Обществознание,
автор: Алёнка999
Предмет: Математика,
автор: Агулья