Question

Прямая m симметрична прямой t: y = 2x+4 относительно прямой s: y = (x-3)/3. Написать уравнение прямой m.

Answer 1

Находим коэффициенты наклона прямых
k₁ = 2,  k₂ = 1/3.
Находим угол между прямыми по формуле
tg α = (k₂ - k₁)/(1 + k₂*k₁ =(- 1 2/3)/(1+ 2/3) = - 1
α = arctg(-1) = - 45°
По этой же формуле находим коэффициент третьей, симметричной, прямой.
tg β = (k₃ - k₂)/(1 + k₂*k₃) = - 1 - находим k₃.
k₃ - 1/3 = - 1 + 1/3*k₃
2/3*k₃ = - 2/3
k3 = - 1
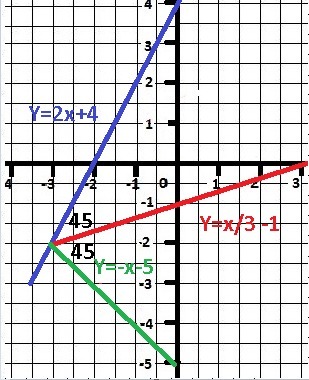
Уравнение прямой m - Y = -x - 5 - ОТВЕТ
Рисунок в приложении подтверждает расчет.