Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, найти производную
Приложения:
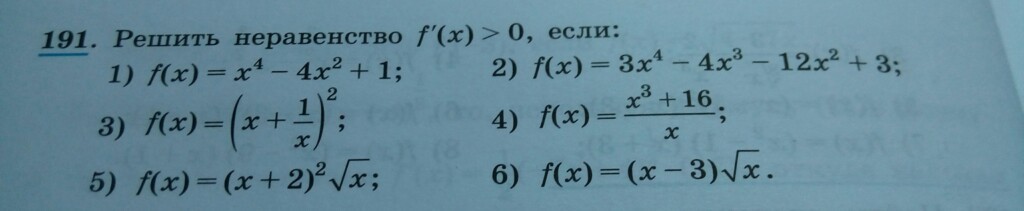
Ответы
Автор ответа:
0
1) f(x) = x⁴ - 4x² + 1
f'(x) = 4x³ - 8x
4x³ - 8x > 0
4x(x² - 2) > 0
4x(x - √2)(x + √2) > 0
С помощью метода интервалов получаем:
-√2 < x < 0 и x > √2
Ответ: (-√2; 0) ∪ (√2; +∞)
2) f(x) = 3x⁴ - 4x³ - 12x² + 3
f'(x) = 12x³ - 12x² - 24x
12x³ - 12x² - 24x > 0
x³ - x² - 2x > 0
x(x² - x -2) > 0
x(x + 1)(x - 2) > 0
С помощью метода интервалов получаем:
-1 < x < 0 и x > 2
Ответ: (-1; 0) ∪ (2; +∞)
3)

С помощью метода интервалов получаем:
-1 < x < 0 и x > 1
Ответ: (-1; 0) ∪ (1; +∞)
4)

С помощью метода интервалов получаем:
x > 2
Ответ: (2; +∞)
5) f(x) = (x + 2)²√x
f'(x) = ((x + 2)²)'√x + (x+2)²(√x)' = 2(x+2)√x + (x² + 4x + 4)1/2√x

С помощью метода интервалов получаем:
x > 0
Ответ: (0; +∞)
6) f(x) = (x - 3)√x

С помощью метода интервалов получаем:
x > 1
Ответ: (1; +∞)
f'(x) = 4x³ - 8x
4x³ - 8x > 0
4x(x² - 2) > 0
4x(x - √2)(x + √2) > 0
С помощью метода интервалов получаем:
-√2 < x < 0 и x > √2
Ответ: (-√2; 0) ∪ (√2; +∞)
2) f(x) = 3x⁴ - 4x³ - 12x² + 3
f'(x) = 12x³ - 12x² - 24x
12x³ - 12x² - 24x > 0
x³ - x² - 2x > 0
x(x² - x -2) > 0
x(x + 1)(x - 2) > 0
С помощью метода интервалов получаем:
-1 < x < 0 и x > 2
Ответ: (-1; 0) ∪ (2; +∞)
3)
С помощью метода интервалов получаем:
-1 < x < 0 и x > 1
Ответ: (-1; 0) ∪ (1; +∞)
4)
С помощью метода интервалов получаем:
x > 2
Ответ: (2; +∞)
5) f(x) = (x + 2)²√x
f'(x) = ((x + 2)²)'√x + (x+2)²(√x)' = 2(x+2)√x + (x² + 4x + 4)1/2√x
С помощью метода интервалов получаем:
x > 0
Ответ: (0; +∞)
6) f(x) = (x - 3)√x
С помощью метода интервалов получаем:
x > 1
Ответ: (1; +∞)
Похожие вопросы
Предмет: Алгебра,
автор: rinauleva161
Предмет: Қазақ тiлi,
автор: ernuroralbekov
Предмет: Химия,
автор: mariakasiyan
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: АленкаБуза