помогите!12,13.............
Ответы
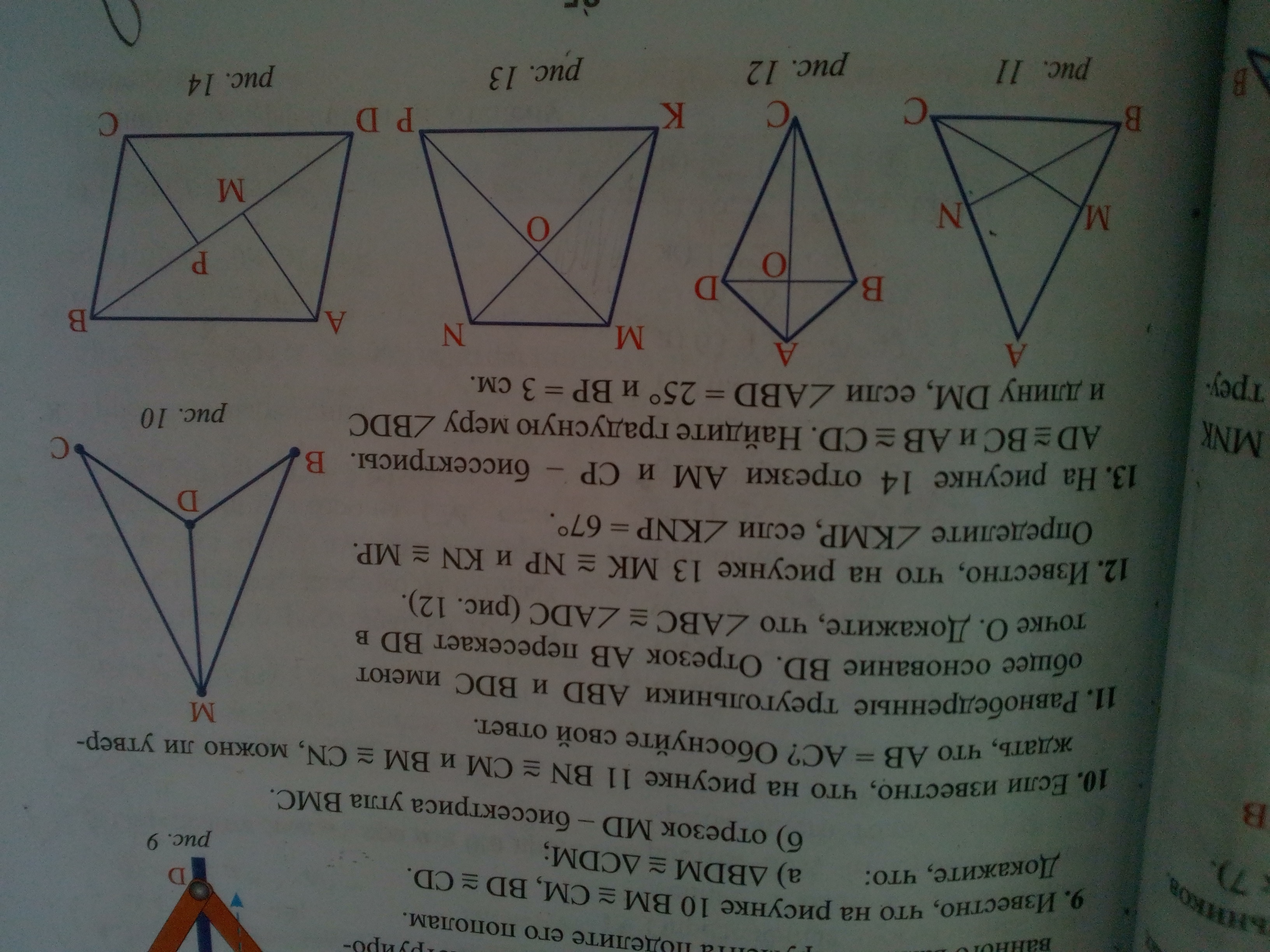
Задача 12.
Дано:
MK = NP; KN = MP;
<KNP = 67°;
Найти <KMP.
Решение.
Рассмотрим ∆КМN и ∆PNM, у них:
1) MK = NP по условию;
2) KN = MP по условию;
3) KP - общая
Если три стороны одного треугольника равны трём сторонам другого треугольника, то эти треугольники равны: ∆КМN = ∆PNM.
Из равенства треугольников следует равенство соответственных элементов, значит, <KMP = <KNP = 67°.
Ответ: <KМP = 67°.
Задача 13.
Дано:
AM и CP - биссектрисы;
AD = BC; AB = CD;
<ABD = 25°;
BP = 3 см.
Найти <BDC; DM.
Решение.
1). Рассмотрим ∆ABD и ∆CBD, у них:
1)AD = BC - по условию;
2) AB = CD - по условию;
3) BD - общая
Если три стороны одного треугольника равны трём сторонам другого треугольника, то эти треугольники равны: ∆ABD = ∆CBD .
Из равенства треугольников следует равенство соответственных элементов:
<ABD = <BDC = 25°;
<ADB = <DBC
<DAВ = <DCB.
2) Каждый из равных углов <DAВ = <DCB разделён биссектрисами АМ и СР на равные углы:
<DAM = <MАB = <DCP = <PCB.
3) Рассмотрим ∆BPC и ∆AMD.
1)AD = BC - по условию;
2) <BCP = <DAM;
3) <ADB = <DBC
Если сторона и два прилегающих угла одного треугольника равны стороне и двум прилегающим углам другого треугольника, то эти треугольники равны: ∆BPC = ∆AMD.
Из равенства треугольников следует равенство соответственных сторон: BР = DМ = 3 см.
Ответ: <BDC = 25°; DM = 3 см.
.