Предмет: Алгебра,
автор: TaissaFarmiga
докажите торжество
arctg(1/2)+arcctg(1/3)=pi/4
Приложения:
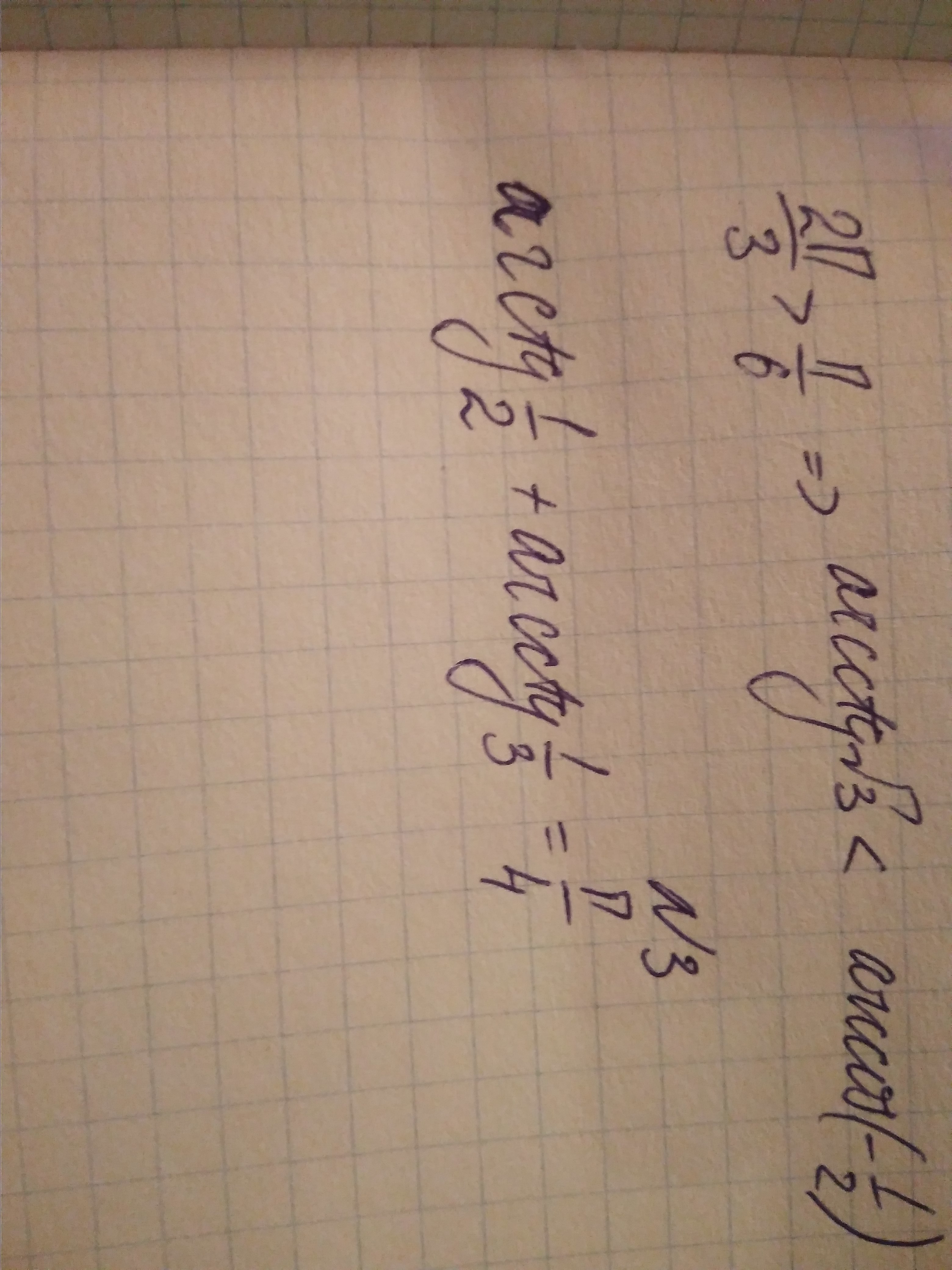
Ответы
Автор ответа:
0
task/26323516
--------------------
Докажите тождество :
arctg(1/2) + arcctg(1/3) = π /4
---------------------
Пусть arctg(1/2) + arcctg(1/3)= φ
* * * tg(α + β) = ( tgα + tgβ) / (1 -tgα *tgβ ) * * *
tgφ = tg( arctg1/2 + arcctg1/3 ) =tg( arctg1/2 + arctg3 )
( tg( arctg1/2) +tg( arctg3) ) / (1 - tg( arctg1/2) *tg( arcctg3 ) ) =
= (1/2 +3) /(1 -(1/2)*3) =3,5 /(-0,5) = - 7 . φ ≠ π/4 ⇒ пример неверно .
========================================
Верное тождество : arctg(1/2) + arctg(1/3) = π /4 .
φ = arctg1/2 + arctg1/3
tgφ = tg( arctg1/2 + arctg1/3 ) =
( tg( arctg1/2 +tg( arctg1/3 ) / (1 -tg( arctg1/2) *tg( arctg1/3 ) ) =
= (1/2 +1/3) / ( 1 -(1/2)*(1/3) ) = (5 /6 ) / (5/6) = 1 . ⇒ φ = π/4 .
--------------------
Докажите тождество :
arctg(1/2) + arcctg(1/3) = π /4
---------------------
Пусть arctg(1/2) + arcctg(1/3)= φ
* * * tg(α + β) = ( tgα + tgβ) / (1 -tgα *tgβ ) * * *
tgφ = tg( arctg1/2 + arcctg1/3 ) =tg( arctg1/2 + arctg3 )
( tg( arctg1/2) +tg( arctg3) ) / (1 - tg( arctg1/2) *tg( arcctg3 ) ) =
= (1/2 +3) /(1 -(1/2)*3) =3,5 /(-0,5) = - 7 . φ ≠ π/4 ⇒ пример неверно .
========================================
Верное тождество : arctg(1/2) + arctg(1/3) = π /4 .
φ = arctg1/2 + arctg1/3
tgφ = tg( arctg1/2 + arctg1/3 ) =
( tg( arctg1/2 +tg( arctg1/3 ) / (1 -tg( arctg1/2) *tg( arctg1/3 ) ) =
= (1/2 +1/3) / ( 1 -(1/2)*(1/3) ) = (5 /6 ) / (5/6) = 1 . ⇒ φ = π/4 .
Похожие вопросы
Предмет: Українська мова,
автор: alisaprvt8
Предмет: Информатика,
автор: jcrjrvjrgrgh
Предмет: Қазақ тiлi,
автор: Arystanbek43
Предмет: История,
автор: got5
Предмет: Математика,
автор: КлубничкаНика