Предмет: Алгебра,
автор: TheRastaPlay
Решите неравенство, номер 138-139. Тема: решение иррациональных неравенств и их систем. Примеры в фото ниже:
Приложения:
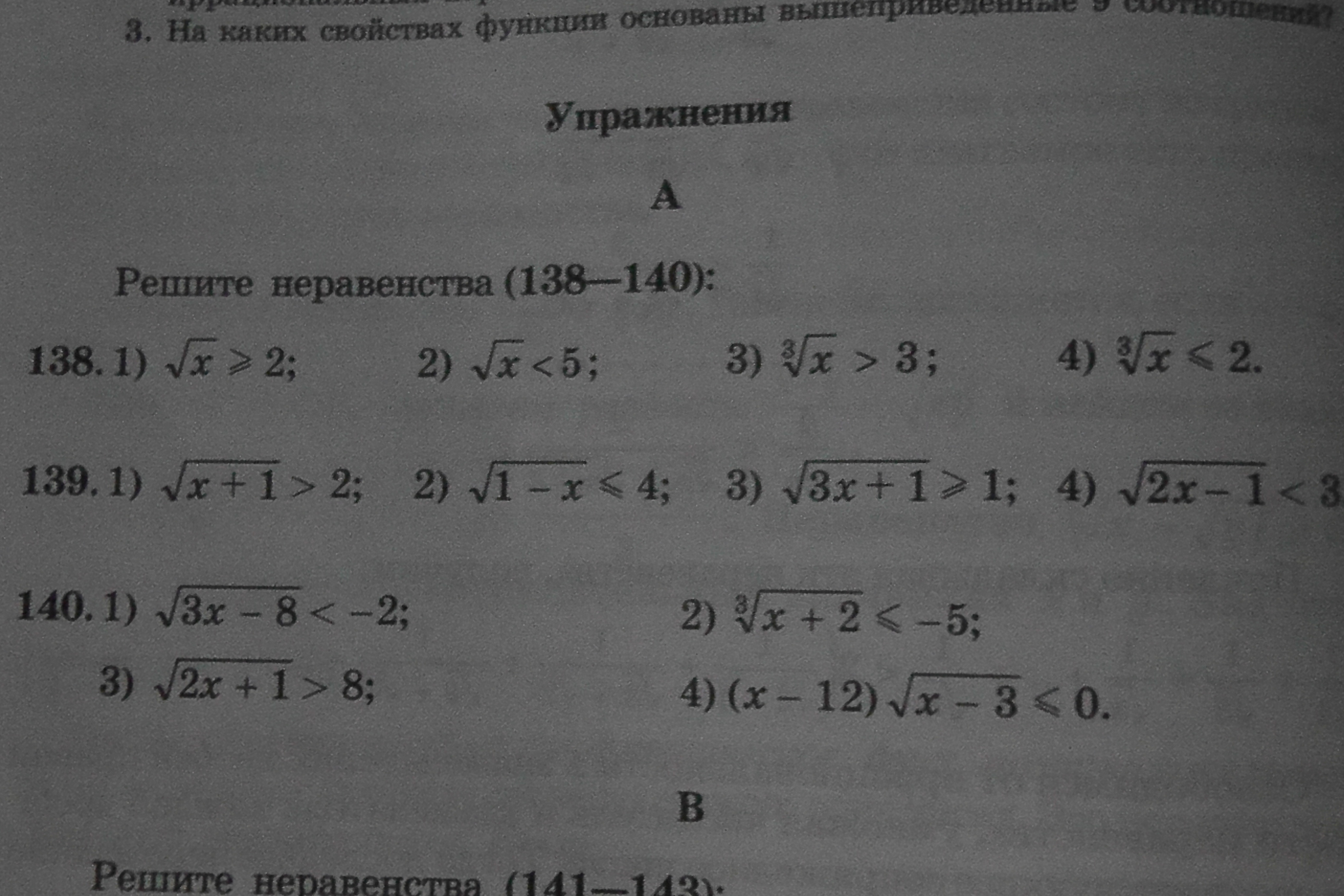
Ответы
Автор ответа:
0
task/26315157
-------------------
138.
-------
1)
√x ≥2 ⇔ x ≥ 2² ⇔ x∈[2 ; ∞).
2)
√x < 5 ⇔ 0≤ x <5² ⇒ x∈ [0 ; 25) .
3)
∛x >3 ⇔x >3³ ⇒ x∈ [27 ; ∞ ).
4)
∛x ≤ 2 ⇔x ≤2³ ⇒ x∈ ( -∞ ; 8 ].
----------------------------------------
139.
-------
1)
√(x+1) >2 ⇔x+1 >2² ⇔ x > 4 -1 ⇔x ∈ (3 ;∞).
2)
√(1-x) ≤4 ⇔ 0 ≤ 1- x ≤ 4² ⇔ -16 ≤ x -1 ≤0 ⇔ -15 ≤ x ≤ 1 ⇔x ∈ [-15;1].
3)
√(3x+1) ≥1 ⇔ 3x+1 ≥1² ⇔ 3x ≥0 ⇔ x ≥ 0 ⇔x ∈ [0;∞].
4)
√(2x-1) < 3 ⇔ 0 ≤ 2x -1 < 3² ⇔ 1 ≤ 2x < 3² + 1⇔ 1/2 ≤ x <5 ⇔x ∈ [0,5;5).
-------------------
138.
-------
1)
√x ≥2 ⇔ x ≥ 2² ⇔ x∈[2 ; ∞).
2)
√x < 5 ⇔ 0≤ x <5² ⇒ x∈ [0 ; 25) .
3)
∛x >3 ⇔x >3³ ⇒ x∈ [27 ; ∞ ).
4)
∛x ≤ 2 ⇔x ≤2³ ⇒ x∈ ( -∞ ; 8 ].
----------------------------------------
139.
-------
1)
√(x+1) >2 ⇔x+1 >2² ⇔ x > 4 -1 ⇔x ∈ (3 ;∞).
2)
√(1-x) ≤4 ⇔ 0 ≤ 1- x ≤ 4² ⇔ -16 ≤ x -1 ≤0 ⇔ -15 ≤ x ≤ 1 ⇔x ∈ [-15;1].
3)
√(3x+1) ≥1 ⇔ 3x+1 ≥1² ⇔ 3x ≥0 ⇔ x ≥ 0 ⇔x ∈ [0;∞].
4)
√(2x-1) < 3 ⇔ 0 ≤ 2x -1 < 3² ⇔ 1 ≤ 2x < 3² + 1⇔ 1/2 ≤ x <5 ⇔x ∈ [0,5;5).
Автор ответа:
0
Благодарю Вас!
Похожие вопросы
Предмет: Музыка,
автор: rusanovatoma339
Предмет: Английский язык,
автор: asylhan887sai76
Предмет: История,
автор: denenot2007
Предмет: Химия,
автор: miakax
Предмет: Математика,
автор: selina2005