Предмет: Математика,
автор: Kerasfs
Найдите производную (подробное решение): ((2x-1)^2)*sqrt(1-2x)
Приложения:
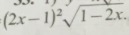
Ответы
Автор ответа:
0
=
=
Похожие вопросы