Предмет: Математика,
автор: Dno142
Определите сколько общих точек имеет окружность (х+6)^2+(у-4)^2=25
а) С осью Ох
б) С осью Оу
в) Прямой у=8
г) Прямой х=-1
Ответы
Автор ответа:
0
a) С осью Ох , т.е y=0 , тогда

Корни уравнения

Получаем точки пересечения с осью OX
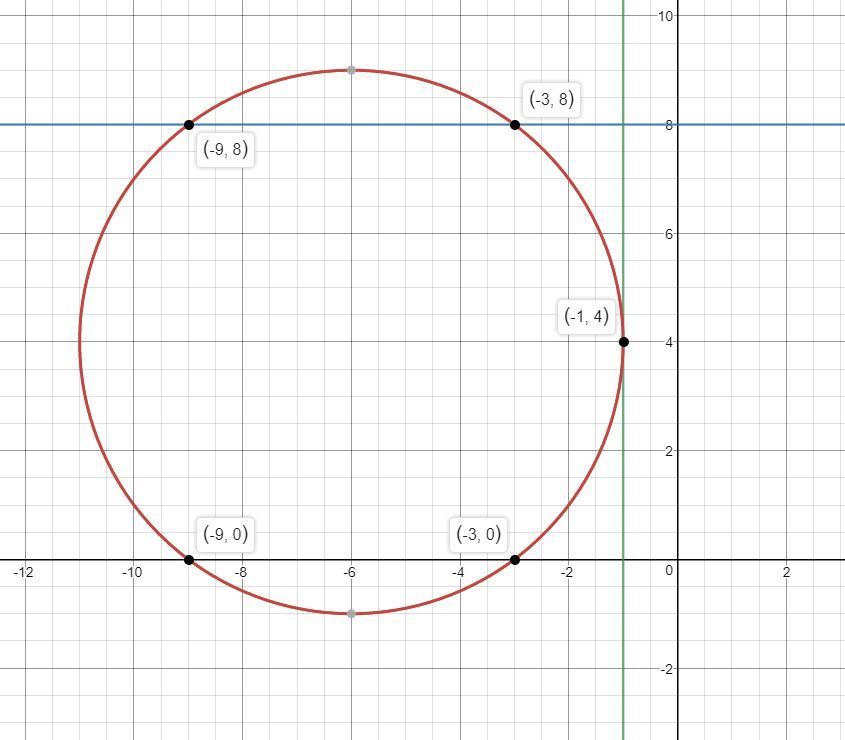
(-3 ; 0) и (-9 ; 0)
б) С осью Оу

Дискриминант меньше ноля D < 0, корней нет!
Значит пересечение с осью OY - нет!
в) С прямой у=8

Корни уравнения

Получаем точки пересечения с прямой y=8
(-3 ; 8) и (-9 ; 8)
г) С прямой x=-1

Получаем только одну точку с прямой х=-1
(-1 ; 4)
Корни уравнения
Получаем точки пересечения с осью OX
(-3 ; 0) и (-9 ; 0)
б) С осью Оу
Дискриминант меньше ноля D < 0, корней нет!
Значит пересечение с осью OY - нет!
в) С прямой у=8
Корни уравнения
Получаем точки пересечения с прямой y=8
(-3 ; 8) и (-9 ; 8)
г) С прямой x=-1
Получаем только одну точку с прямой х=-1
(-1 ; 4)
Приложения:
Автор ответа:
0
Огромное спасибо!
Похожие вопросы
Предмет: История,
автор: nicolechalamet
Предмет: Английский язык,
автор: Kisat84
Предмет: Алгебра,
автор: angelinabazenova83
Предмет: Математика,
автор: helga21
Предмет: Литература,
автор: викуляпобеда