Question

Радиус окружности, описанной вокруг правильного n-угольника, равен 6 см, а радиус вписанной - 3√2 см. Найти кол-во сторон многоугольника и их длину.

Answer 1

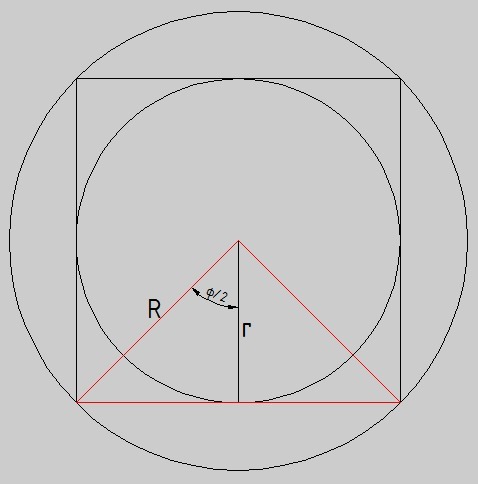
из центра окружностей опустим радиус к внутренней окружности, перпендикулярно ему построим касательную к вписанной окружности до пересечения с описанной. Это будет одна сторона правильного многоугольника.
Вычислим угол ф под которым она видна из центра 
cos(ф/2) = r/R = 3√2/6 = √2/2
ф/2 = arccos(√2/2) = Pi/4
ф = Pi/2 = 90°
Количество сторон правильного многоугольника равно 360/ф = 360/90 = 4
Это квадрат :)