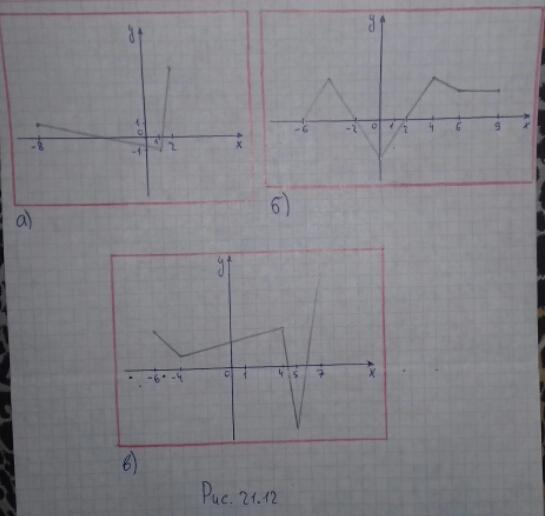
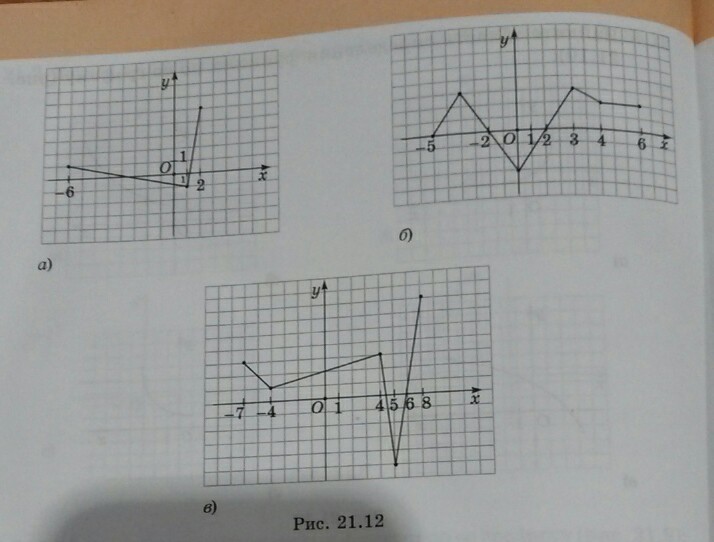
по графику функции, изображенному на рисунке 21. 12 Найдите:
1) область определения функции;
2) значение аргумента, при котором функция равна нулю;
3) числовые промежутки, на которых функция: а) возрастает; б) убывает.
Ответы
На координатной плоскости для каждой оси задаётся единичный отрезок. Не может быть такого, что с одного конца оси одна клетка равна единице, а с другого конца двойке. Однако на графиках не соблюдается ед. отрез. и не понятно, когда именно клетка изменила своё значение. Поэтому к этому решению я прикреплю графики с правильными обозначениями. Ещё условие указано не полность, полное условие я тоже прикреплю.
Решение:
Рисунок 21.12 график а).
1) Область определения: D(y)=[-8;2];
2) x при которых функция равна нулю (координаты точек, пересечения графика с осью Ox, по оси Ox):
3) x при которых функция:
а) Возрастает (чем больше x, тем больше y речь про координаты): x∈[1;2];
б) Убывает (чем больше x, тем меньше y): x∈[-8;1];
4) x при которых функция:
а) Положительная (график выше оси Ox):
б) Отрицательная (график ниже оси Ox):
Рисунок 21.12 график б).
1) D(y)=[-6;9];
2) y=0: x={-6;-2;2};
3)
а) y↑: x∈[-6;-4]∪[0;4];
б) y↓: x∈[-4;0]∪[4;6];
4)
а) y>0: x∈(-6;-2)∪(2;9];
б) y<0: x∈(-2;2).
Рисунок 21.12 график в).
1) D(y)=[-6;7];
2) y=0:
3)
а) y↑: x∈[-4;4]∪[5;7];
б) y↓: x∈[-6;-4]∪[4;5];
4)
а) y>0:
б) y<0:
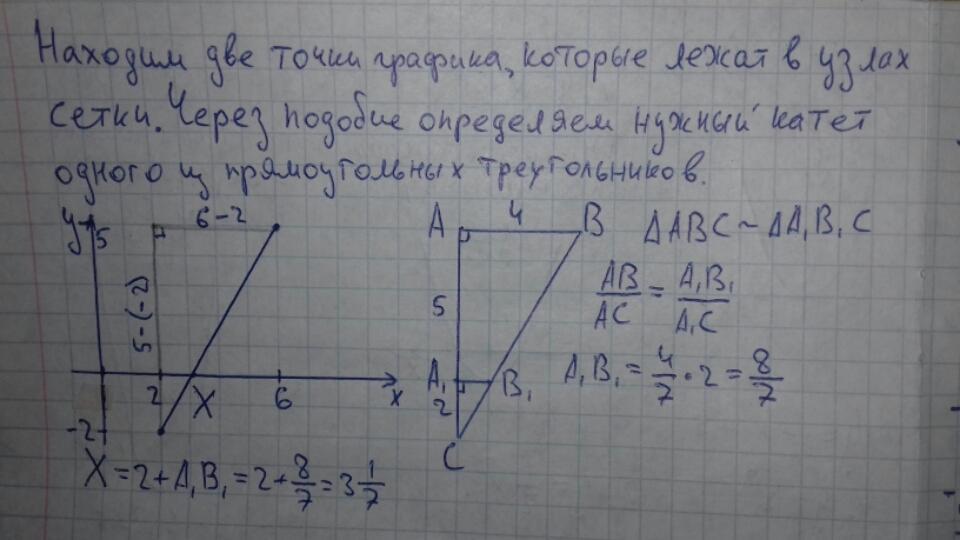
Как точно по клеткам определить нули ломанной или прямой, по графику, я расписал в последнем прикреплённом файле.