Question

Диагонали прямоугольника ABCD пересекаются в точке O. Угол ABD = 64. Найдите угол COD и AOD. СРОЧНО!

Answer 1

Ответ:

128°,  52°

Объяснение:

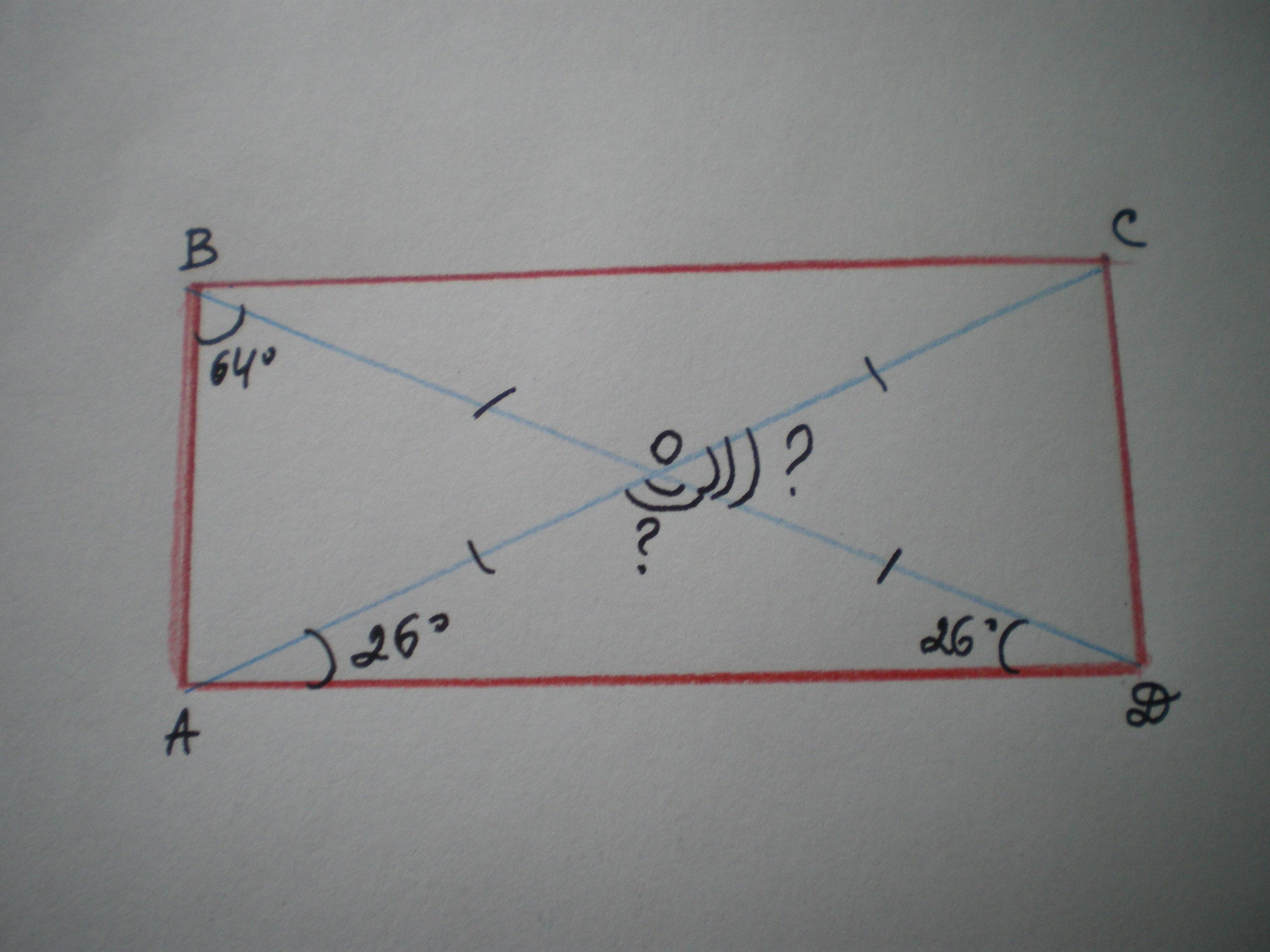
Дано: ABCD - прямоугольник, AB и CD - диагонали, ∠ABD=64°.

Найти ∠COD и AOD.

Диагонали прямоугольника равны и в точке пересечения делятся пополам.

Рассмотрим ΔABD - прямоугольный.

Сумма острых углов прямоугольного треугольника составляет 90°, поэтому ∠ADВ=90-64=26°

Рассмотрим ΔАОD - равнобедренный, т.к. АО=ОD по свойству диагоналей прямоугольника.

Значит, ∠ОАD=∠ОDА=26°.

∠АОD=180-(26+26)=128°

∠АОD и ∠СОD - смежные, их сумма составляет 180°, поэтому

∠СОD=180-128=52°