Предмет: Математика,
автор: gleb20000507
Исследуйте функцию f(x) с помощью производной и постройте график.
f(x)=x^3+6x^2+9x
f(x)=x^4-10x^2+9
Прошу,отправьте ответы фотографией.
Приложения:


Ответы
Автор ответа:
0
ДАНО
Y = x³+6*x²+9x
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞)
2. Пересечение с осью Х. Y=0 при х1 = -3, х2=х3=0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) = -x³+6x² -9x ≠ Y(x).
Функция ни чётная ни нечётная.
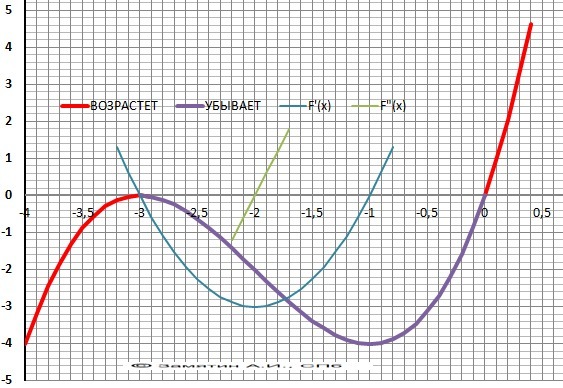
6. Производная функции.Y'(x)= 3*x²+12*x+9.
7. Корни : Y'(x) = 0 при x1=-3 и x2 = 0 .
Максимум Ymax(-3) =0 , минимум – Ymin(0)= -4.
Возрастает - Х∈(-∞;-3)∪(-1;+∞) , убывает = Х∈(-3;-1).
8. Вторая производная - Y"(x) = 6x+12.
9. Точка перегибаY"(x)=0 при X=-2.
Выпуклая “горка» Х∈(-∞;-2),
Вогнутая – «ложка» Х∈(-2;+∞).
10. График в приложении.
Y = x³+6*x²+9x
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞)
2. Пересечение с осью Х. Y=0 при х1 = -3, х2=х3=0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) = -x³+6x² -9x ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x²+12*x+9.
7. Корни : Y'(x) = 0 при x1=-3 и x2 = 0 .
Максимум Ymax(-3) =0 , минимум – Ymin(0)= -4.
Возрастает - Х∈(-∞;-3)∪(-1;+∞) , убывает = Х∈(-3;-1).
8. Вторая производная - Y"(x) = 6x+12.
9. Точка перегибаY"(x)=0 при X=-2.
Выпуклая “горка» Х∈(-∞;-2),
Вогнутая – «ложка» Х∈(-2;+∞).
10. График в приложении.
Приложения:
Автор ответа:
0
Второе задание где?
Автор ответа:
0
Теперь и не будет ответа
Похожие вопросы
Предмет: Физика,
автор: filimonenkova7
Предмет: Математика,
автор: muradovasabina25
Предмет: Информатика,
автор: piplil616
Предмет: Математика,
автор: Помоги1231