Предмет: Математика,
автор: Бодя386
Оценить выражение: 7-5cos^2 x
Приложения:
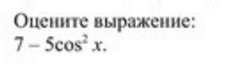
Ответы
Автор ответа:
0
Известно, что cost ≤ 1, т.е. -1 ≤ cost ≤ 1, поэтому:
-1 ≤ cos²x ≤ 1
-5 ≤ 5cos²x ≤ 5
-5 ≤ -5cos²x ≤ 5
1 ≤ 7 - 5cos²x ≤ 12
-1 ≤ cos²x ≤ 1
-5 ≤ 5cos²x ≤ 5
-5 ≤ -5cos²x ≤ 5
1 ≤ 7 - 5cos²x ≤ 12
Автор ответа:
0
(cosx)^2 не может быть от -5, только от нуля, потому что квадрат - число неотрицательное.
Автор ответа:
0
0≤(cosx)^2≤1
Автор ответа:
0
Возможно, моё решение неверное, я не настаиваю.
Автор ответа:
0
7-5(cosx)^2
0≤cosx≤1
0≤(cosx)^2≤1
-5≤-5(cosx)^2≤0
2≤7-5(cosx)^2≤7
0≤cosx≤1
0≤(cosx)^2≤1
-5≤-5(cosx)^2≤0
2≤7-5(cosx)^2≤7
Автор ответа:
0
-1≤cosx≤1
Автор ответа:
0
В общем, в качестве решения напиши вот эти 3 строчки:
0≤(cosx)^2≤1
-5≤-5(cosx)^2≤0
2≤7-5(cosx)^2≤7
0≤(cosx)^2≤1
-5≤-5(cosx)^2≤0
2≤7-5(cosx)^2≤7
Похожие вопросы
Предмет: Физика,
автор: ekbdbekajshhsajjs
Предмет: Биология,
автор: cholodoimelovek1
Предмет: Українська мова,
автор: polishbondar63
Предмет: Физика,
автор: Walker40
Предмет: Математика,
автор: polinaprilepska