Question

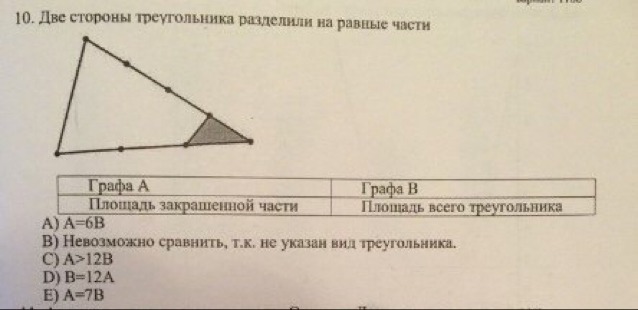
Две стороны треугольника разделили на равные части

Answer 1

Ответ: В=12 А.

Объяснение: 

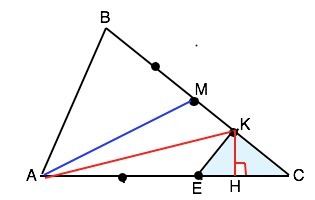
Обозначим вершины целого треугольника АВС, закрашенной части –ЕКС. 

Примем площадь ∆АВС=S. 

Проведем отрезок АМ к середине ВС. 

Медиана делит площадь треугольника на треугольники с равной площадью. ⇒ 

 Площадь ∆ АМС=S/2. 

МК=КС по условию. АК- медиана ∆ АМС. ⇒

 Площадь Δ АКС=S/2•1/2=S/4

Высота КН - общая для ∆ АКС и Δ ЕКС. 

Площади треугольников с равными высотами относятся как длины их оснований. 

Ѕ ∆ ЕКС=13 Ѕ ∆ АКС ⇒

Ѕ ∆ ЕКС=(S/4):3=S/12 --

S∆ ABC=12 Ѕ ∆ EКC