Предмет: Алгебра,
автор: FortAgarti
Срочно! Изобразите на координатной плоскости множество точек , задаваемые неравенством:
а) |y-x-1|<2
б)x²+(y+1)²>=4
Пожалуйста распишите решение)
Ответы
Автор ответа:
0
б) если рассмотреть равенство: x² + (y+1)² = 4
то график этого уравнения --это окружность с центром в (0; -1) радиуса 2.
уравнение окружности с центром (x₀; y₀) радиуса R: (х-х₀)² + (y-y₀)² = R²
в задании знак неравенства "больше", т.е. это часть плоскости ВНЕ круга, включая границу (окружность)
например: точка (2;-3)
2² + (-3+1)² ≥ 4 верно...
а) неравенство с модулем со знаком "меньше" равносильно двойному неравенству: -2 < y-x-1 < 2 (прибавим 1)
-1 < y-x < 3
двойное неравенство равносильно системе неравенств (пересечению промежутков):
{y-x<3
{y-x>-1
или
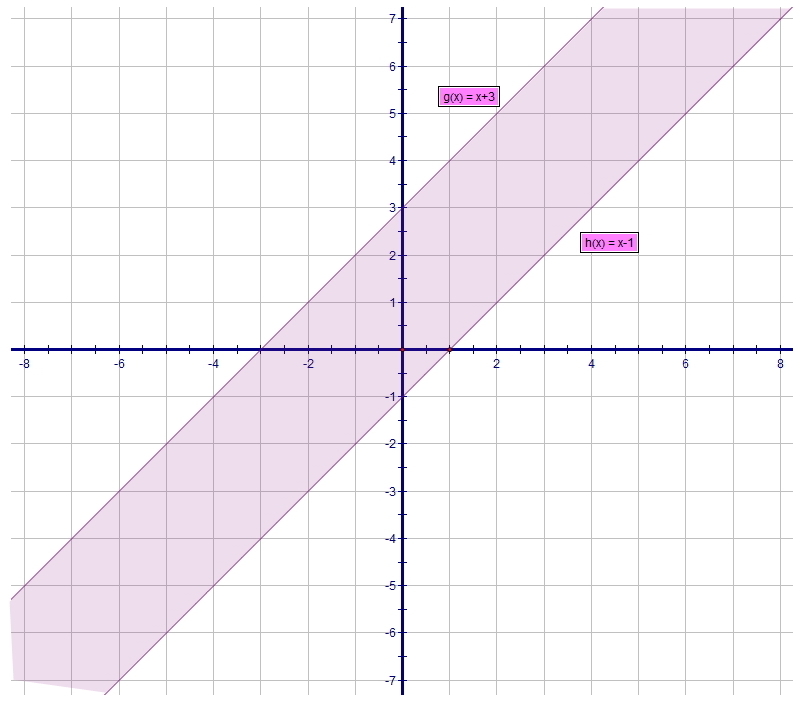
{ y < x+3 (часть плоскости НИЖЕ (знак "<") прямой у=х+3)
{ y > x-1 (часть плоскости ВЫШЕ (знак ">") прямой у=x-1)
это полоса между параллельными прямыми...
и всегда можно проверить...
например, точка (2;-1) не принадлежит этому множеству...
|-1-2-1| < 2 неверно
точка (0;0) принадлежит этому множеству...
|0-0-1| < 2 верно
то график этого уравнения --это окружность с центром в (0; -1) радиуса 2.
уравнение окружности с центром (x₀; y₀) радиуса R: (х-х₀)² + (y-y₀)² = R²
в задании знак неравенства "больше", т.е. это часть плоскости ВНЕ круга, включая границу (окружность)
например: точка (2;-3)
2² + (-3+1)² ≥ 4 верно...
а) неравенство с модулем со знаком "меньше" равносильно двойному неравенству: -2 < y-x-1 < 2 (прибавим 1)
-1 < y-x < 3
двойное неравенство равносильно системе неравенств (пересечению промежутков):
{y-x<3
{y-x>-1
или
{ y < x+3 (часть плоскости НИЖЕ (знак "<") прямой у=х+3)
{ y > x-1 (часть плоскости ВЫШЕ (знак ">") прямой у=x-1)
это полоса между параллельными прямыми...
и всегда можно проверить...
например, точка (2;-1) не принадлежит этому множеству...
|-1-2-1| < 2 неверно
точка (0;0) принадлежит этому множеству...
|0-0-1| < 2 верно
Приложения:

Автор ответа:
0
Спасибо большое
Автор ответа:
0
рада была помочь))
Похожие вопросы
Предмет: Английский язык,
автор: Sveta060121
Предмет: Математика,
автор: tanaguseva2809
Предмет: Химия,
автор: Kosta126238
Предмет: Обществознание,
автор: игокряк
Предмет: Математика,
автор: полина340