Предмет: Алгебра,
автор: maserdaser
АААА СРОЧНО, ПОМОГИТЕ ПОСЧИТАТЬ
Приложения:
Ответы
Автор ответа:
0
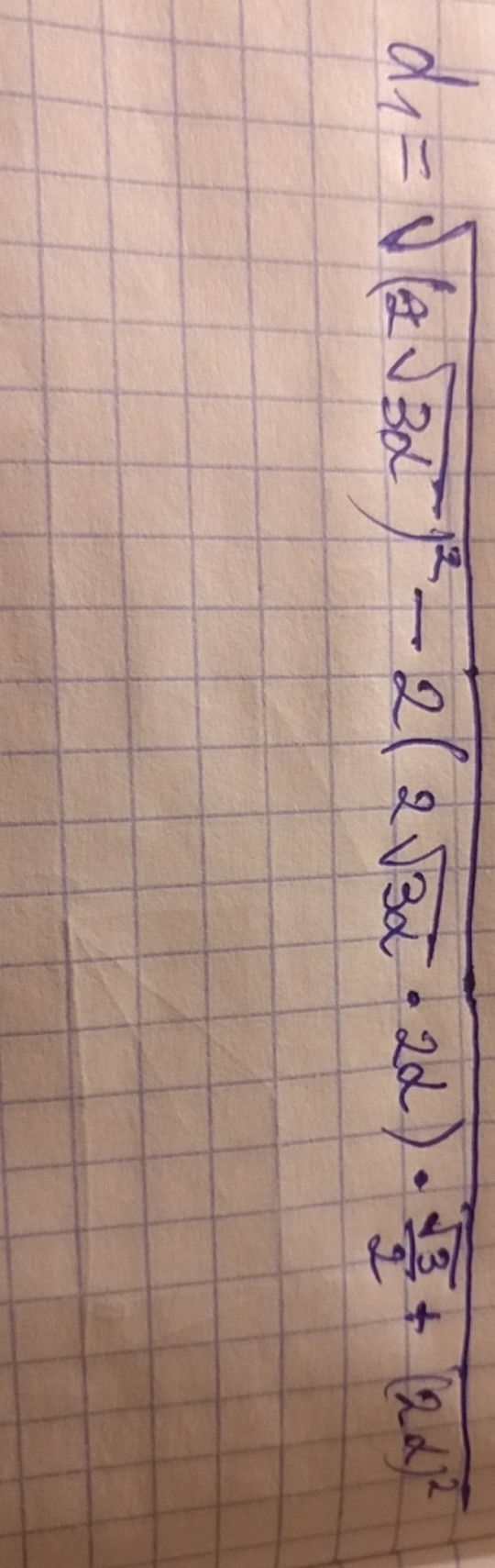
d₁ = √((2√3d)² - 2(2√(3d) · 2d) · √3/2 + (2d)²) = √(2√(3d) · (2√3d) -(4 · √(4 · 3b) ·
· 4d) · √3/2 + 4d²) = √(√(2²3d) · √(2²3d) -(√(16 · 12d) · 4d) · √3/2 + 4d²) =
= √(√(4 · 3d) · √(4 · 3d) - (√(192d) · 4d · √3/2) + 4d²) = √((√(12d) · √(12d)) -
- (√(192d) · (4d · √3)/2) + 4d²) = √(√(12d · 12d) - (√(192d) · (2d · √3)) + 4d²) =
= √(√(144d²) - (√(192d) · √(4d² · 3)) + 4d²) = √(√(12d)² - (√(192d · 4d² · 3) +
+ 4d² = √(12d - √(768d³ · 3) + 4d²) = √(12d - √(2304d³) + 4d²) = √(12d -
- (√2304 · √d² · √d) + 4d²) = √(12d - (48 · d · d^1/2) + 4d²) = √(12d - 48d^(1/1 +
+ 1/2) + 4d²) = √(12d - 48d^(2/2 + 1/2) + 4d²) = √(12d - 48d^3/2 + 4d²) =
= √4d(3 - 14d^1/2 + d) = √4d · √(d - 14√d + 3) = 2√d · √(d - 14√d + 3) =
= 2√(d(d - 14√d + 3)) = 2√(d² - 14√d³ + 3d)
· 4d) · √3/2 + 4d²) = √(√(2²3d) · √(2²3d) -(√(16 · 12d) · 4d) · √3/2 + 4d²) =
= √(√(4 · 3d) · √(4 · 3d) - (√(192d) · 4d · √3/2) + 4d²) = √((√(12d) · √(12d)) -
- (√(192d) · (4d · √3)/2) + 4d²) = √(√(12d · 12d) - (√(192d) · (2d · √3)) + 4d²) =
= √(√(144d²) - (√(192d) · √(4d² · 3)) + 4d²) = √(√(12d)² - (√(192d · 4d² · 3) +
+ 4d² = √(12d - √(768d³ · 3) + 4d²) = √(12d - √(2304d³) + 4d²) = √(12d -
- (√2304 · √d² · √d) + 4d²) = √(12d - (48 · d · d^1/2) + 4d²) = √(12d - 48d^(1/1 +
+ 1/2) + 4d²) = √(12d - 48d^(2/2 + 1/2) + 4d²) = √(12d - 48d^3/2 + 4d²) =
= √4d(3 - 14d^1/2 + d) = √4d · √(d - 14√d + 3) = 2√d · √(d - 14√d + 3) =
= 2√(d(d - 14√d + 3)) = 2√(d² - 14√d³ + 3d)
Похожие вопросы
Предмет: Алгебра,
автор: cjchchcijfjch
Предмет: История,
автор: elenazobnina781
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: Dacuk2000
Предмет: Математика,
автор: Милая1229