Question

Решите пожалуйста задачу:
В трапеции ABCD диагонали AC и BD взаимно перпендикулярны. AC=15, BD=20. Найдите площадь трапеции.

Answer 1

Так как диагонали и взаимно перпендикулярны, то все четыре треугольника - прямоугольные. Площадь каждого из них равна половине произведения катетов. 

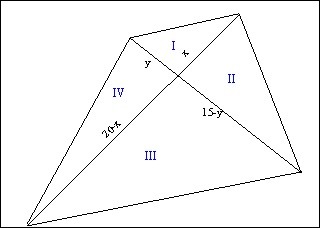
1)Найдём площадь каждого  треугольника (смотри рисунок ниже).
I треугольник 
S₁ = ¹/₂ xy
II треугольник 
S₂ = ¹/₂ x(15-y)
III треугольник 
S₃ = ¹/₂ (20-x)(15-y)
IV треугольник 
S₄ = ¹/₂ (20-x)y

2) Площадь всей трапеции S равна сумме площадей четырёх прямоугольных треугольников:
S = S₁+S₂+S₃+S₄

S = ¹/₂ *ху + ¹/₂ *х(15-у) + ¹/₂ *(20-х)(15-у) + ¹/₂*(20-х)у =

= ¹/₂ * (ху+15х-ху+300-15х-20у+ху+20у-ху) =

= ¹/₂ * 300=150 - площадь трапеции.

Ответ: S = 150