Предмет: Геометрия,
автор: marselina1
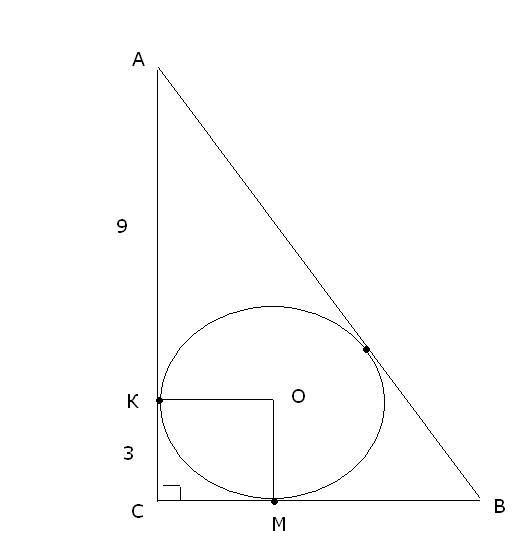
В прямоугольный треугольник вписали круг. Точка соприкосновения делит один из катетов на отрезки длинною 3 см и 9 см, начиная от вершины прямого угла. Найдите другой катет и гипотенузу
Ответы
Автор ответа:
0
Баллов, конечно, маловато. Обозначим треугольник АВС. С- прямой угол. Точки соприкосновения со стороной АС назовем К, а со стороной СВ - М. Заметим, что АС=АК+КС=9+3=12 см. Заметим, что СКОМ - квадрат, так как ОК перпендикулярно АС - так как АС - касательная к вписанной окружности. С - прямой угол по условию задачи. ОМ перпендикулярно СВ, так как СВ - касательная к вписанной окружности. На оставшийся угол КОМ остается 90 градусов по свойству сумм углов четырехугольника в евклидовой геометрии. Сумма углов четырехугольника равна 360 градусам. 3 известных угла -прямые, значит на четвертый угол КОМ остается 360-3*90=360-270=90градусов. Заметим, что СК=ОК=3 см. Значит длина радиуса вписанной окружности равна 3 см. Площадь прямоугольного треугольника равна половине произведения катетов. S=0,5AC*CB=0,5*12*CB=6CB (1).
С другой стороны S=p*r, где r - радиус вписанной окружности, р - полупериметр.
S=3*p.
S=3*0,5*(AC+CB+AB).
S=3*0,5*(12+CB+AB).
По теореме Пифагора
Или

Значит по-другому

Приравняем правые части уравнений (1) и (2). Найдем катет СВ.

Сократим обе части на 3.

Умножим обе части на 2



Возведем обе части в квадрат

Сократим обе части на слагаемое 144.

Перенесем все в одну часть


Сократим обе части на 8.


Первый ответ СВ=0 - не подходит по смыслу задачи. Второй ответ СВ=9 см - подойдет.
Гипотенузу вычислим по той же теореме Пифагора





AB=15 см
Ответ: неизвестный катет равен СB=9 см, гипотенуза равна AB=15 см.
С другой стороны S=p*r, где r - радиус вписанной окружности, р - полупериметр.
S=3*p.
S=3*0,5*(AC+CB+AB).
S=3*0,5*(12+CB+AB).
По теореме Пифагора
Или
Значит по-другому
Приравняем правые части уравнений (1) и (2). Найдем катет СВ.
Сократим обе части на 3.
Умножим обе части на 2
Возведем обе части в квадрат
Сократим обе части на слагаемое 144.
Перенесем все в одну часть
Сократим обе части на 8.
Первый ответ СВ=0 - не подходит по смыслу задачи. Второй ответ СВ=9 см - подойдет.
Гипотенузу вычислим по той же теореме Пифагора
AB=15 см
Ответ: неизвестный катет равен СB=9 см, гипотенуза равна AB=15 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kalasnikovm000
Предмет: Алгебра,
автор: haskyksu
Предмет: Информатика,
автор: knstntnde
Предмет: Алгебра,
автор: maryam9
Предмет: Биология,
автор: t4esg