Question

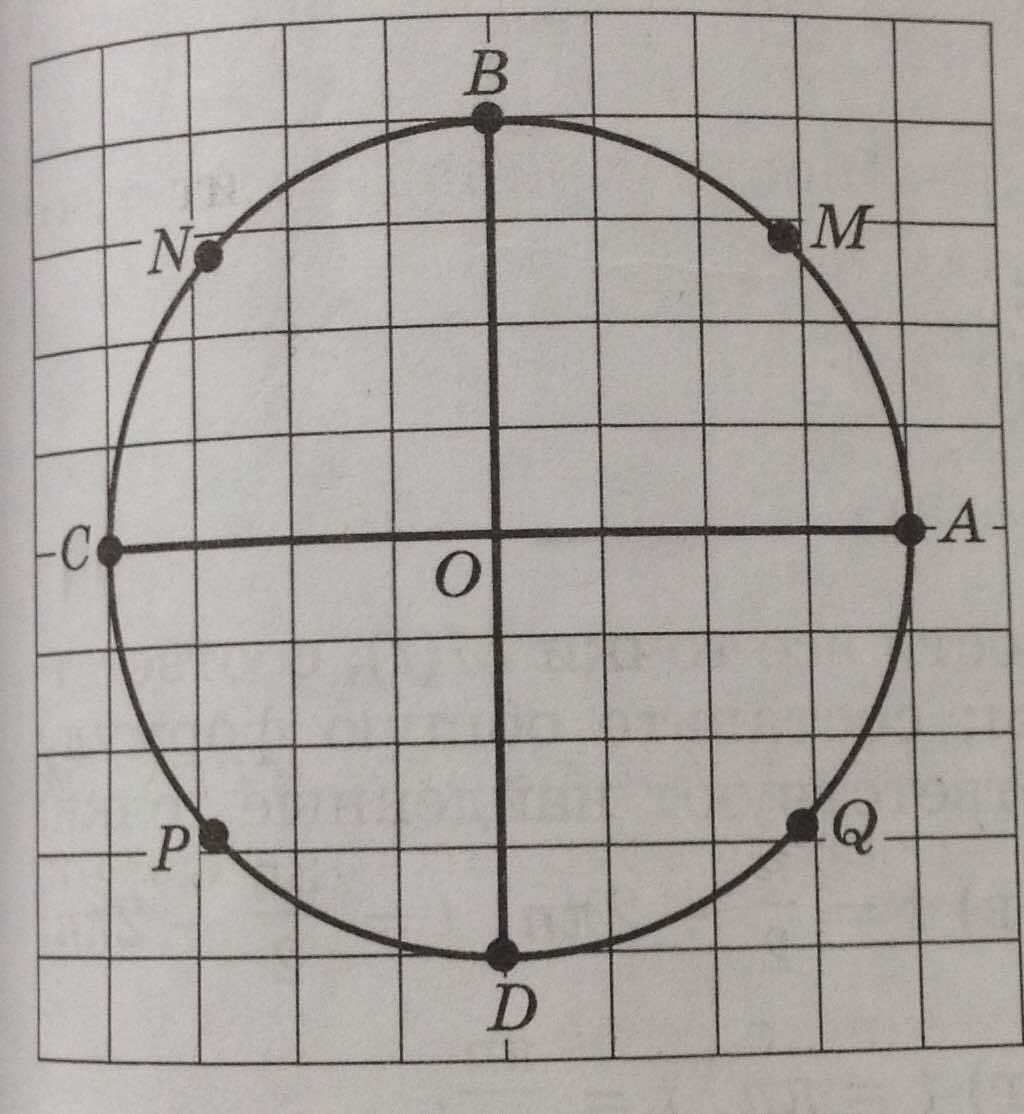
Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие указанному объединению дуг BC ∪ DA. Пожалуйста, помогите, напишите решение, а то ответ в учебнике есть, а я не понимаю.

Answer 1

На промежутке [0;2π]:

Точка B - $tt frac{pi }2$;

Точка C - π;

Дуга BC - $tt begin{bmatrix}frac{pi }2 ;pi end{bmatrix}$;

Точка D - $tt frac{3pi }2$;

Точка A - 2π;

Дуга DA - $tt begin{bmatrix}frac{3pi }2 ;2pi end{bmatrix}$.

Значит объединению дуг BC и DA соответствуют числа $tt tin begin{bmatrix}frac{pi }2 +2pi k;pi +2pi kend{bmatrix} cup begin{bmatrix}frac{3pi }2 +2pi k;2pi +2pi kend{bmatrix} ,kin mathbb{Z}$ т.к. целый круг это 2π.

Точки B,C и D,A диаметрально противоположны (отличаются на π), а период (2π) кратен π, поэтому объединение промежутков можно упростить и представить как $tt begin{bmatrix}frac{pi }2 +pi k;pi +pi kend{bmatrix} ,kin mathbb{Z}$

У промежутка период π, поэтому концы промежутка без периода могут отличаться на π (одновременно), то есть ответов может быть множество.

Ответ: $tt displaystyle begin{bmatrix}frac{pi }2 +pi k;pi +pi kend{bmatrix} ,kin mathbb{Z}$