Question

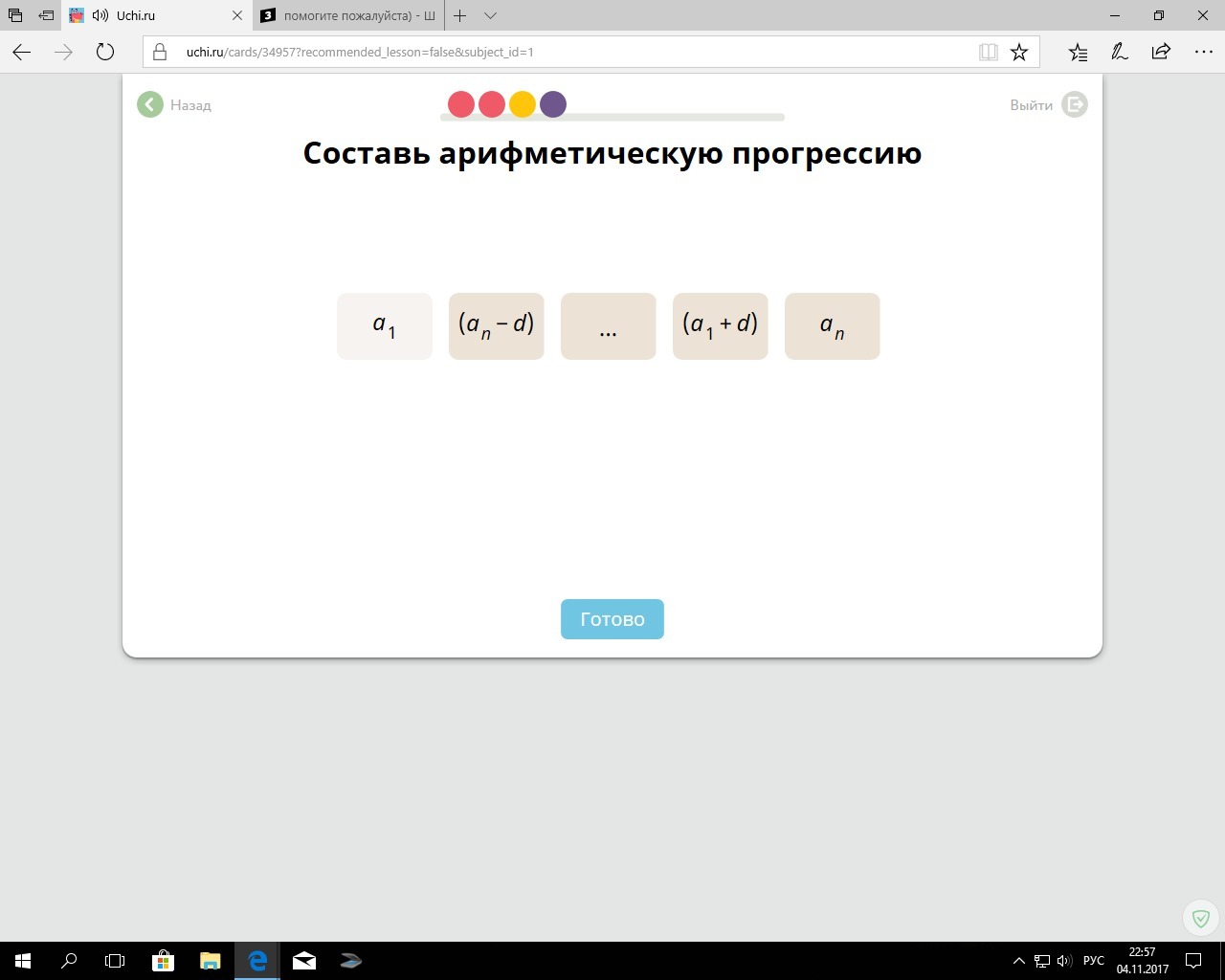
помогите пожалуйста)

Answer 1

d=a(n)-a(1)+d
2d=a(n)-a(1)
d=(a(n)-a(1))/2

a(2)=a(n)-d=a(n)-(a(n)-a(1))/2=(a(n)+a(1))/2
a(n-1)=a(1)+d=a(1)+(a(n)-a(1))/2=(a(n)+a(1))/2
получается, что второй и (n-1) члены арифметической прогрессии равны: a(2)=a(n-1), а значит d=0:
(a(n)-a(1))/2=0
a(n)-a(1)=0
a(n)=a(1)

a(1) a(1) ... a(1) a(1)

Answer 2

а еще лучше поменять местами второй и (n-1) члены прогрессии (вторую клеточку с четвертой), тогда она хотя бы точно станет прогрессией.