Question

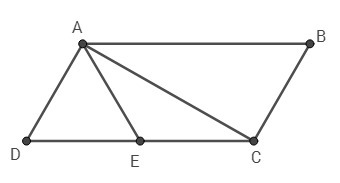
В параллелограмме ABCD точка E середина CD. Площадь трапеции AECB равна 102. Найдите площадь ABCD.

Answer 1

Проведем диагональ АС.
DE = EC ⇒ AE - медиана ΔDAC
Медиана разбивает треугольник на два треугольника одинаковой площади ⇒ $S_{DAE}=S_{EAC}$
Пусть $S_{DAE}=S_{EAC} = x$ , тогда $S_{DAC} = 2x$

Диагональ параллелограмма делит его на два равных треугольника ⇒
$S_{ABC}=S_{DAC}=2x$

$S_{ABCE} =S_{ABC}+S_{EAC}= 2x+x=3x \ 3x=102 \ x= 34 \ \ S_{ABCD}=S_{ABCE}+S_{DAE}=102+34=136$

Ответ: 136 кв.ед.