Question

нарисовать заданные линии или области: Im(1/z) < -1/2

Answer 1

z = x + iy
1/z = 1/(x + iy) = (x - iy)/(x^2 + y^2)
Im(1/z) = -y/(x^2 + y^2)

-y/(x^2 + y^2) < 1/2
y/(x^2 + y^2) > 1/2
x^2 + y^2 < 2y
x^2 + (y^2 - 2y + 1) < 1
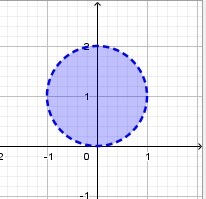
x^2 + (y - 1)^2 < 1 — это уравнение внутренности окружности с центром в точке (0, 1) и радиусом 1