Предмет: Математика,
автор: Vladislav1603
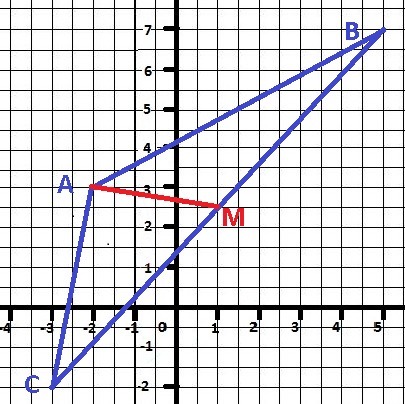
Определить острый угол между высотой и медианой
треугольника ABC, проведенными из вершины A, если
координаты вершин известны: A(-2, 3), B(5, 7) и C(-3, -2).
Ответы
Автор ответа:
0
Сделаем решение графическим методом.
Рисунок к задаче - в приложении.
РЕШЕНИЕ
Координата точки М - медианы
Мх = Сх +(Вх - Сх)/2 = 1
Му = Су + (Ву - Су)/2 = 2,5
Уравнение медианы - прямая АМ.
k = (Aу - Му)/(Ах - Мх) = - 1/6
b = Ау - k*Ax = 2 2/3
Уравнение прямой АМ - Y = - 1/6*x + 2 2/3
Уравнение прямой АВ
Y = 4/7 *x + 4 1/7
Угол между прямыми АВ и АМ - острый.
tg α = (k2 - k1)/(1 + k1*k2) = - 0.738/0.904 = - 0.816
arctg α = -0.6843
α ≈39.2° - ОТВЕТ
Рисунок к задаче - в приложении.
РЕШЕНИЕ
Координата точки М - медианы
Мх = Сх +(Вх - Сх)/2 = 1
Му = Су + (Ву - Су)/2 = 2,5
Уравнение медианы - прямая АМ.
k = (Aу - Му)/(Ах - Мх) = - 1/6
b = Ау - k*Ax = 2 2/3
Уравнение прямой АМ - Y = - 1/6*x + 2 2/3
Уравнение прямой АВ
Y = 4/7 *x + 4 1/7
Угол между прямыми АВ и АМ - острый.
tg α = (k2 - k1)/(1 + k1*k2) = - 0.738/0.904 = - 0.816
arctg α = -0.6843
α ≈39.2° - ОТВЕТ
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ravilovaevelina27
Предмет: Русский язык,
автор: esanovrasul373
Предмет: Алгебра,
автор: stefuninsvitlana
Предмет: Информатика,
автор: Kolok2016
Предмет: Биология,
автор: Nikitohka1