Question

y=-3sin5x+1 E(y)?
Объясните,пожалуйста,как находить множество это?

Answer 1

E(y) - множество значений функции y.
В данном случае у нас есть sin(5x).
-1≤sin(5x)≤1
(-3)*(-1)≥-3sin(5x)≥(-3)*1
3≥-3sin(5x)≥-3
3+1≥-3sin(5x)+1≥-3+1
4≥-3sin5x+1≥-2

Сама функция y непрерывна (является суммой произведения непрерывных функций, а сумма непрерывных функций и произведение непрерывных функций - непрерывные функции), а значит принимает все промежуточные значения. Значения 4 и -2 достижимы (4 - например, при x=3, -2 - например, при x=1)

Ответ: y∈[-2;4]

Answer 2

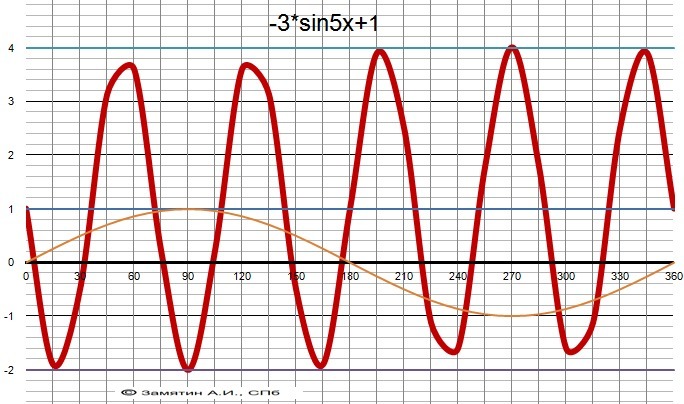
График функции - в приложении.
Известно, что функция Sin x - периодическая с областью значений - Е∈[-1;1].
При умножении аргумента на 5х - амплитуда не меняется. Изменился только период функции.
При умножении на  3 - амплитуда увеличилась в три раза и стала - E∈[-3;3].
При сдвиге на +1 - изменяются обе границы области - 
-3+1 = -2 ≤ У(х) ≤ 3+1 = 4.
Окончательно  - E∈[-2;4] - ОТВЕТ