Предмет: Алгебра,
автор: Skvrtsvs
Найдите значение производной функции
Приложения:
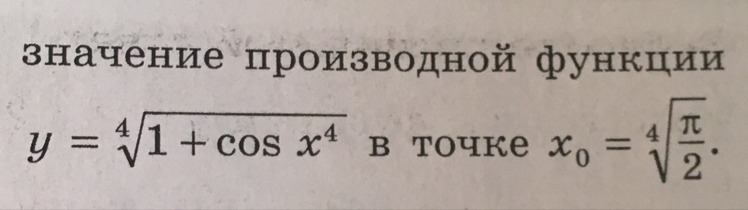
Ответы
Автор ответа:
0
Автор ответа:
0
в условии х0 = корень из пи/2 (у вас пи/4)
Автор ответа:
0
О нет! Как же так вышло?
Похожие вопросы
Предмет: Информатика,
автор: duchhdcbn
Предмет: Физика,
автор: wiaien
Предмет: Математика,
автор: pascalrozalina
Предмет: Литература,
автор: inobek