Предмет: Математика,
автор: IFender
Найти общее решение дифференциального уравнения
Приложения:
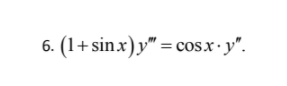
Ответы
Автор ответа:
0
Автор ответа:
0
Добрый вечер, можете решить такое? https://znanija.com/task/26392401 не могу разобраться, пожалуйста
Похожие вопросы
Предмет: Окружающий мир,
автор: inkarm32
Предмет: Литература,
автор: mnedyhalov
Предмет: Алгебра,
автор: sonya8151
Предмет: Литература,
автор: nimerciukn
Предмет: Математика,
автор: Аноним