Предмет: Математика,
автор: troi4ka
Помогите Привести к каноническому виду уравнения линий второго порядка. Сделать чертежи.
Приложения:
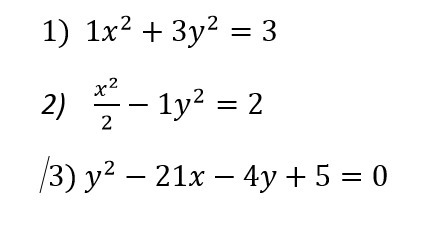
Ответы
Автор ответа:
0
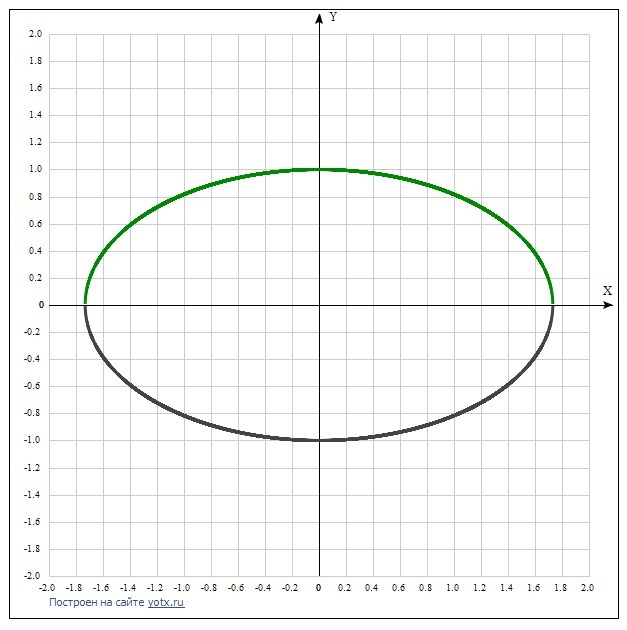
1) Разделим обе части уравнения на 3 и получаем каноническое уравнение эллипса:
(x^2/3) + (y^2/1) = 1.
2) Разделим обе части уравнения на 2 и получаем каноническое уравнение гиперболы:
(x^2/4) - (y^2/2) = 1.
3) Выделяем полные квадраты:
для y1:
(y1²-2*2y1 + 2²) -1*2² = (y1-2)²-4
Преобразуем исходное уравнение:
(y1-2)² = 21x -1
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y-2)² = 2*(21/2)(x - (1/21)).
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке ((1/21);2)
Параметр p = -21/2
Координаты фокуса:

Уравнение директрисы: x = x0 - p/2
x = (1/21) - (21/4) = -437/84.
(x^2/3) + (y^2/1) = 1.
2) Разделим обе части уравнения на 2 и получаем каноническое уравнение гиперболы:
(x^2/4) - (y^2/2) = 1.
3) Выделяем полные квадраты:
для y1:
(y1²-2*2y1 + 2²) -1*2² = (y1-2)²-4
Преобразуем исходное уравнение:
(y1-2)² = 21x -1
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y-2)² = 2*(21/2)(x - (1/21)).
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке ((1/21);2)
Параметр p = -21/2
Координаты фокуса:
Уравнение директрисы: x = x0 - p/2
x = (1/21) - (21/4) = -437/84.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: tanboyar
Предмет: Математика,
автор: kira9299
Предмет: Физика,
автор: lerasplaytab
Предмет: Алгебра,
автор: zhoramaksimov
Предмет: Математика,
автор: mama16021977