Предмет: Математика,
автор: iskusnykhvlada
Номер 3
Все примеры (1-5)
Пожалуйста, срочно!!!!
Приложения:
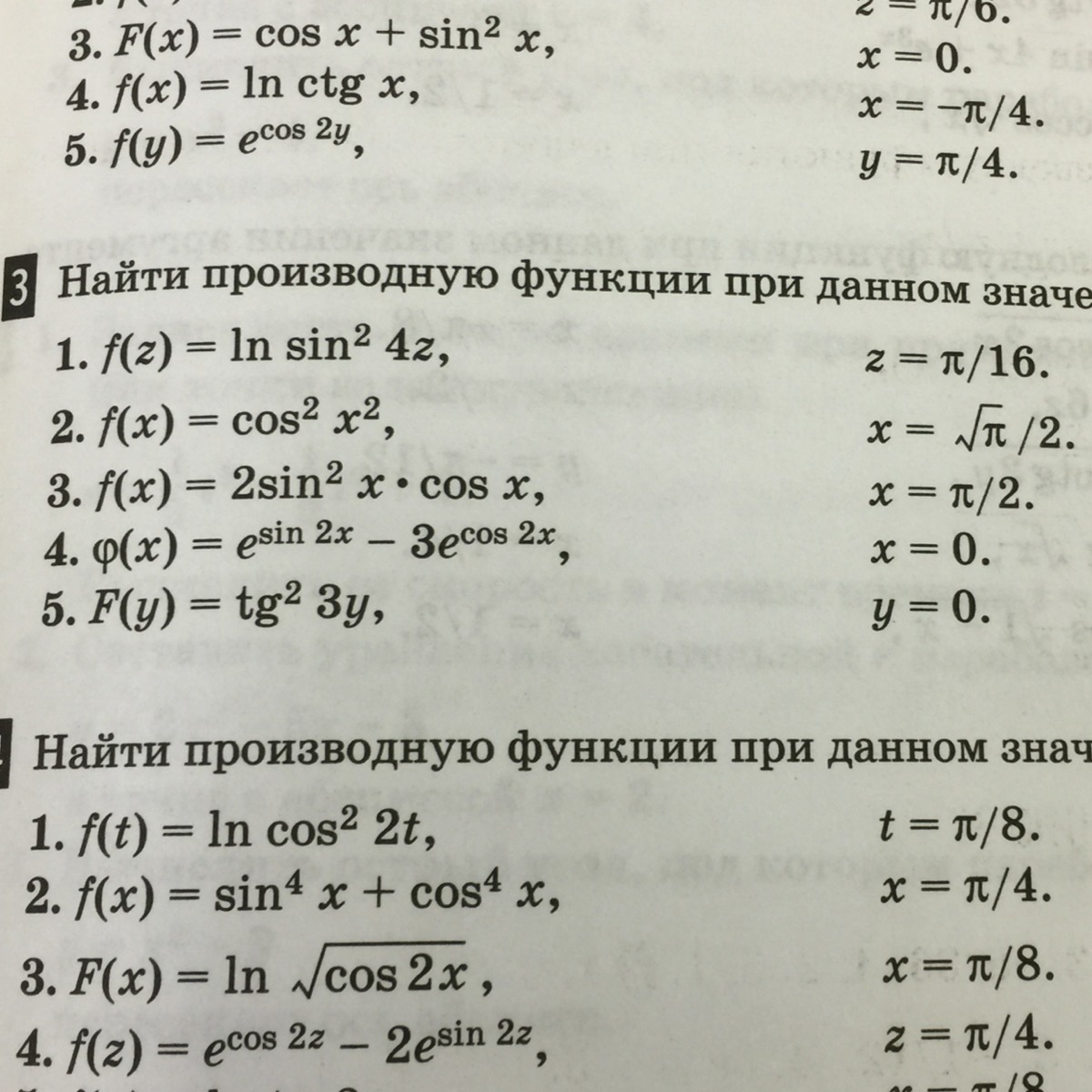
Ответы
Автор ответа:
0
1) f'(z)= 2 /(sin4z) ·4 cos 4z =8(cos 4z)/(sin4z)
при z=π/16 f'(π/16)=8(cos 4·π/16)/(sin4·π/16) =8
2) (cos²x²)'= 2(cosx²)·(-sinx²)·2x=-4cosx²sinx²=-2sin2x²
при x=(√π)/2 (cos²x²)'=-2sin(2(√π)/2)²)=-2sin (π/2)=-2
3) (2(sin²x)(cosx))'=2[(sin²x)'·(cosx)+(sin²x)·(cosx)']=
2[2(sinx)·(cosx)·(cosx)+(sin²x)·(-sinx)]=4(sinx)·(cos²x)-2sin³x
при x=π/2 4(sinπ/2)·(cos²π/2)-2sin³π/2=0-2= -2
4) (e^(sin2x)-3e^(cos2x)'=2cos2x ·e^(sin2x)-3·(-2sin2x ·e^(cos2x))
при x=0 2cos0 ·e^(sin0)-3·(-2sin0 ·e^(cos0))=2+6·0=2
5) (tg²3y)'=2·tg3y·(1/cos²3y)·3=6(tg3y)/(cos²3y)
при y=0 6(tg0)/(cos²0)=6·0/1=0
при z=π/16 f'(π/16)=8(cos 4·π/16)/(sin4·π/16) =8
2) (cos²x²)'= 2(cosx²)·(-sinx²)·2x=-4cosx²sinx²=-2sin2x²
при x=(√π)/2 (cos²x²)'=-2sin(2(√π)/2)²)=-2sin (π/2)=-2
3) (2(sin²x)(cosx))'=2[(sin²x)'·(cosx)+(sin²x)·(cosx)']=
2[2(sinx)·(cosx)·(cosx)+(sin²x)·(-sinx)]=4(sinx)·(cos²x)-2sin³x
при x=π/2 4(sinπ/2)·(cos²π/2)-2sin³π/2=0-2= -2
4) (e^(sin2x)-3e^(cos2x)'=2cos2x ·e^(sin2x)-3·(-2sin2x ·e^(cos2x))
при x=0 2cos0 ·e^(sin0)-3·(-2sin0 ·e^(cos0))=2+6·0=2
5) (tg²3y)'=2·tg3y·(1/cos²3y)·3=6(tg3y)/(cos²3y)
при y=0 6(tg0)/(cos²0)=6·0/1=0
Похожие вопросы
Предмет: Математика,
автор: Rilons
Предмет: Математика,
автор: anisa38jdjdid
Предмет: Английский язык,
автор: lili15480
Предмет: Математика,
автор: pgalina65
Предмет: Алгебра,
автор: marinaalex1722