Question

Геометрия 7 класс. Задачи и упражнения на готовых чертежах Рабинович,таблица 7.9. Сумма углов треугольника. Номер 10-12

Answer 1

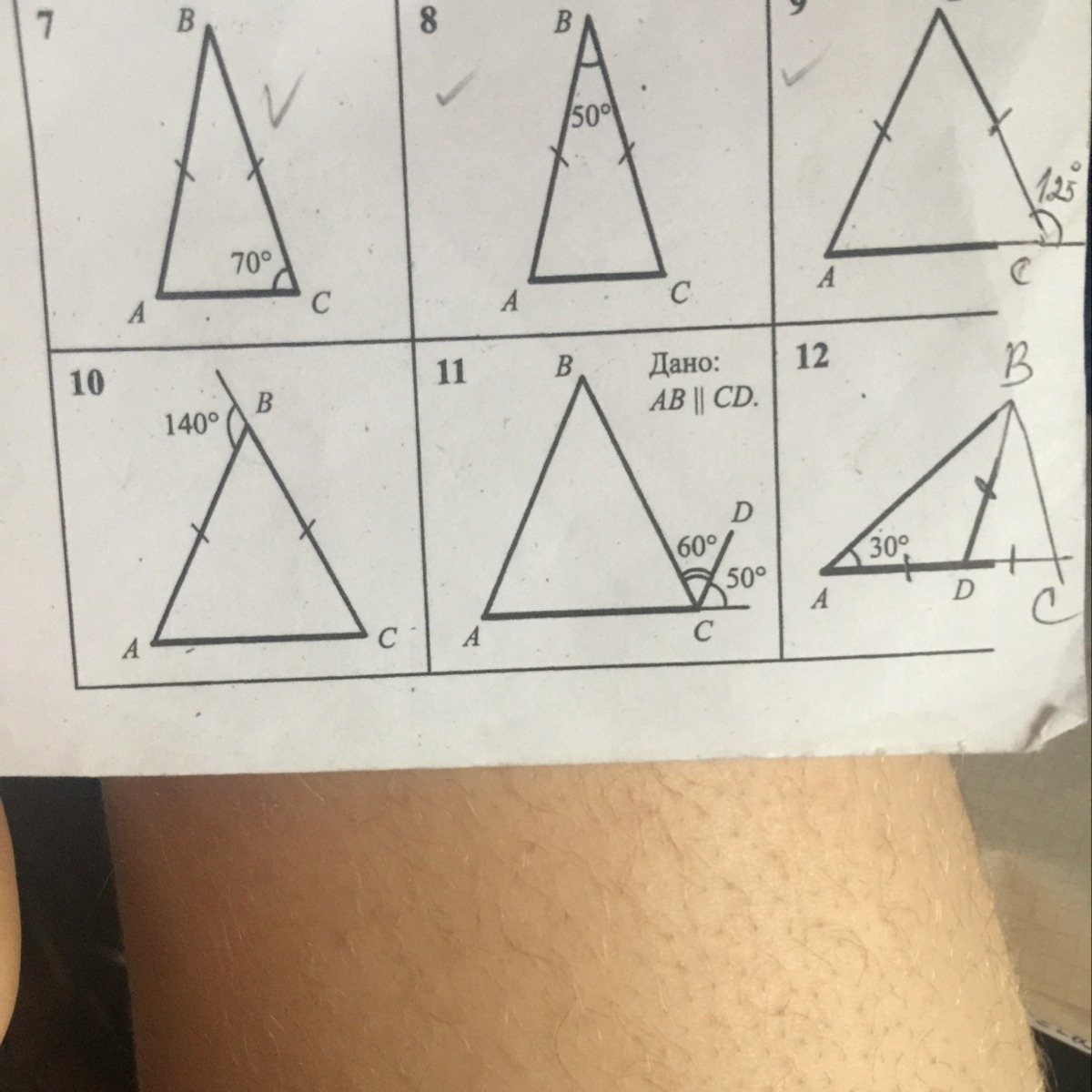
10. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.  140° - внешний угол, значит

∠А + ∠С = 140°

∠А = ∠С = 140°/2 = 70° как углы при основании равнобедренного треугольника.

∠В = 180° - 140° = 40° по свойству смежных углов.

11. ∠А = 50° как соответственные углы при пересечении параллельных прямых АВ и CD секущей АС,

∠В = 60° как накрест лежащие при пересечении параллельных прямых АВ и CD секущей ВС,

∠С = 180° - (60° + 50°) = 180° - 110° = 70° по свойству смежных углов.

12. ∠А = 30°

∠DBA = ∠DAB = 30° как углы при основании равнобедренного треугольника,

∠BDC = ∠DBA + ∠DAB = 30° + 30° = 60° как внешний угол ΔBAD,

∠DBC = ∠DCB = (180° - ∠BDC)/2 = (180° - 60°)/2 = 120°/2 = 60° как углы при основании равнобедренного треугольника BDC.

∠С = 60°

∠АВС = 180° - (∠В + ∠С) = 180° - (30° + 60°) = 90°

∠В = 90°