Предмет: Математика,
автор: aubackirow2012
54 и 55 задание,срочно
Приложения:
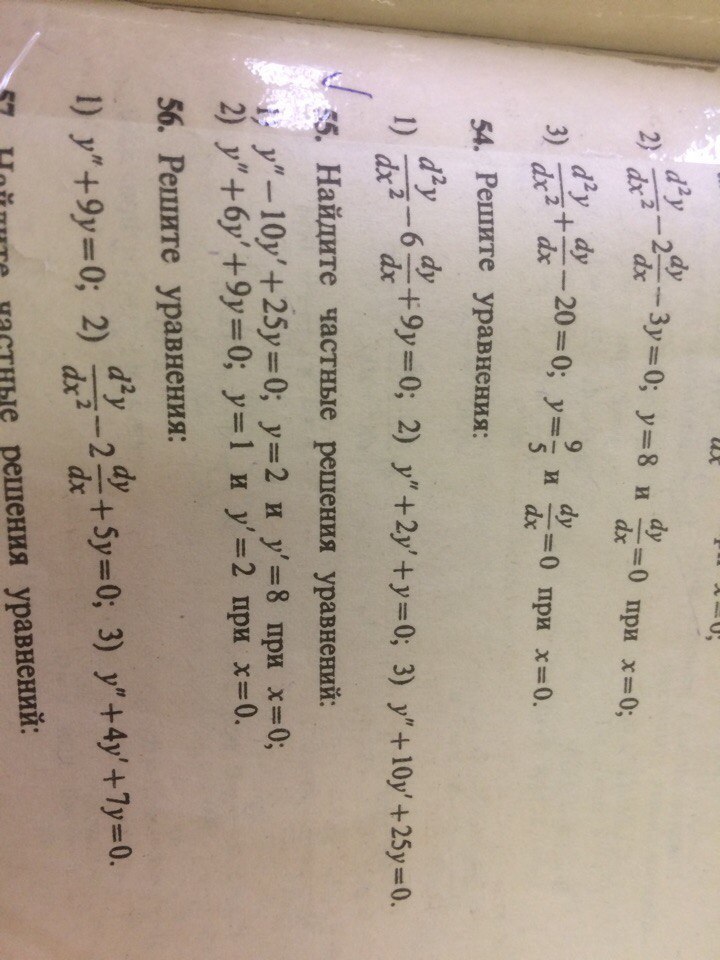
Ответы
Автор ответа:
0
54.
Все три уравнения - линейные ОДУ 2-го порядка.
Для начала нужно будет решить характеристическое уравнение и затем получить решение ОДУ в зависимости от корней характеристического уравнения.
1)


Как мы видим, дискриминант равен 0, а поэтому решение представимо в виде

2)
Все аналогично

3)

55.
Делаем то же самое, но подстановкой данных из условия находим C_1 и C_2
1)

2)

Все три уравнения - линейные ОДУ 2-го порядка.
Для начала нужно будет решить характеристическое уравнение и затем получить решение ОДУ в зависимости от корней характеристического уравнения.
1)
Как мы видим, дискриминант равен 0, а поэтому решение представимо в виде
2)
Все аналогично
3)
55.
Делаем то же самое, но подстановкой данных из условия находим C_1 и C_2
1)
2)
Похожие вопросы
Предмет: Химия,
автор: ashotshymkent
Предмет: Литература,
автор: igumnova2007
Предмет: Обществознание,
автор: sasha7798
Предмет: Обществознание,
автор: DeathValley
Предмет: Математика,
автор: Джессика51240